题目内容
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分别为AB,CD的中点,AE的延长线交CB于F.现将△ACD沿CD折起,折成二面角A-CD-B,连接AF.(I)求证:平面AEF⊥平面CBD;
(II)当二面角A-CD-B为直二面角时,求直线AB与平面CBD所成角的正切值.
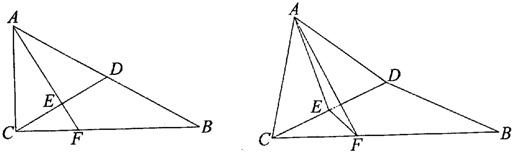
分析:(I)由题意知,△ACD是正三角形,折起后,AE⊥CD,EF⊥CD,故CD⊥平面AEF,从而证明结论.
(II)AE⊥平面CBD,∠ABE就是直线AB与平面CBD所成的角,解直角三角形ABE,可求∠ABE的大小.
(II)AE⊥平面CBD,∠ABE就是直线AB与平面CBD所成的角,解直角三角形ABE,可求∠ABE的大小.
解答: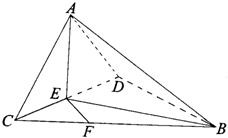 (I)证明:在Rt△ABC中,D为AB的中点,
(I)证明:在Rt△ABC中,D为AB的中点,
得AD=CD=DB,又∠B=30°,得△ACD是正三角形,
又E是CD的中点,得AE⊥CD.(3分)
折起后,AE⊥CD,EF⊥CD,
又AE∩EF=E,AE?平面AED,EF?平面AEF,
故CD⊥平面AEF,(6分)
又CD?平面CDB,
故平面AEF⊥平面CBD.(7分)
(II)解:∵二面角A-CD-B是直二面角,
且AE⊥CD,∴AE⊥平面CBD.(8分)
连接EB,AB,则∠ABE就是直线AB与
平面CBD所成的角.(9分)
设AC=a,在△CDB中,
∠DCB=30°,CE=
,CB=
a,
∴EB2=CE2+CB2-2CE•CB•cos∠DCB=
a2,又AE=
a,在Rt△AEB中,tan∠ABE=
=
=
.
∴直线AB与平面CBD所成角的正切值为
.(14分)
 (I)证明:在Rt△ABC中,D为AB的中点,
(I)证明:在Rt△ABC中,D为AB的中点,得AD=CD=DB,又∠B=30°,得△ACD是正三角形,
又E是CD的中点,得AE⊥CD.(3分)
折起后,AE⊥CD,EF⊥CD,
又AE∩EF=E,AE?平面AED,EF?平面AEF,
故CD⊥平面AEF,(6分)
又CD?平面CDB,
故平面AEF⊥平面CBD.(7分)
(II)解:∵二面角A-CD-B是直二面角,
且AE⊥CD,∴AE⊥平面CBD.(8分)
连接EB,AB,则∠ABE就是直线AB与
平面CBD所成的角.(9分)
设AC=a,在△CDB中,
∠DCB=30°,CE=
| a |
| 2 |
| 3 |
∴EB2=CE2+CB2-2CE•CB•cos∠DCB=
| 7 |
| 4 |
| ||
| 2 |
| AE |
| EB |
| ||||
|
| ||
| 7 |
∴直线AB与平面CBD所成角的正切值为
| ||
| 7 |
点评:证明2个平面垂直,关键在一个平面内找到一条直线和另一个平面垂直,求线面角,关键是找出线在平面内的射影.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=