题目内容
已知圆（x-2）2+（y-3）2=13和圆（x-3）2+y2=9交于A、B两点，则弦AB的垂直平分线的方程是________．
3x+y-9=0
分析：写出过两个圆的方程圆心坐标，两个圆的圆心所在的直线方程，就是AB的垂直平分线的方程．
解答：经过圆（x-2）2+（y-3）2=13和圆（x-3）2+y2=9的圆心坐标分别为（2，3），（3，0），
所以弦AB的垂直平分线的方程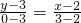
，即3x+y-9=0．
故答案为：3x+y-9=0
点评：本题是基础题，考查圆系方程的有关知识，公共弦所在直线方程，考查计算能力．
分析：写出过两个圆的方程圆心坐标，两个圆的圆心所在的直线方程，就是AB的垂直平分线的方程．
解答：经过圆（x-2）2+（y-3）2=13和圆（x-3）2+y2=9的圆心坐标分别为（2，3），（3，0），
所以弦AB的垂直平分线的方程
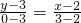，即3x+y-9=0．故答案为：3x+y-9=0
点评：本题是基础题，考查圆系方程的有关知识，公共弦所在直线方程，考查计算能力．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目