题目内容
已知关于x的实系数二次方程x2+ax+b=0有两个实数根α、β,证明:|α|<2且|β|<2是2|a|<4+b且|b|<4的充要条件![]()
见解析
解析:
.证明: (1)(充分性)由韦达定理,得|b|=|α·β|=|α|·|β|<2×2=4![]()
设f(x)=x2+ax+b,则f(x)的图象是开口向上的抛物线![]() 又|α|<2,|β|<2,∴f(±2)>0
又|α|<2,|β|<2,∴f(±2)>0![]()
即有![]() 4+b>2a>-(4+b)又|b|<4
4+b>2a>-(4+b)又|b|<4![]() 4+b>0
4+b>0![]() 2|a|<4+b
2|a|<4+b
(2)必要性![]() 由2|a|<4+b
由2|a|<4+b![]() f(±2)>0且f(x)的图象是开口向上的抛物线
f(±2)>0且f(x)的图象是开口向上的抛物线![]() ∴方程f(x)=0的两根α,β同在(-2,2)内或无实根
∴方程f(x)=0的两根α,β同在(-2,2)内或无实根![]() ∵α,β是方程f(x)=0的实根,∴α,β同在(-2,2)内,即|α|<2且|β|<2
∵α,β是方程f(x)=0的实根,∴α,β同在(-2,2)内,即|α|<2且|β|<2![]()

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
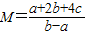 的最小值是 .
的最小值是 .