题目内容
(本小题满分12分)
已知函数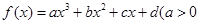 的零点的集合为{0,1},且
的零点的集合为{0,1},且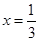 是f(x)的一个极值点。
是f(x)的一个极值点。
(1)求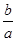 的值;
的值;
(2)试讨论过点P(m,0)与曲线y=f(x)相切的直线的条数。
【答案】
(1)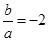 ;(2)当
;(2)当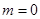 或
或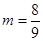 时,
时,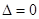 ,方程①有两等根
,方程①有两等根 或
或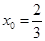 ,此时,过点
,此时,过点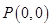 或
或 与曲线
与曲线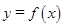 相切的直线有两条;
相切的直线有两条;
当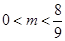 时,
时,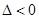 ,方程①无解,此时过点
,方程①无解,此时过点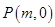 与曲线
与曲线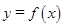 相切的直线仅有一条;
相切的直线仅有一条;
当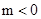 或
或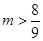 时,
时,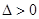 ,方程①有两个不同的实根,此时过点
,方程①有两个不同的实根,此时过点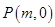 与曲线
与曲线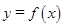 相切的直线有三条.
相切的直线有三条.
【解析】
试题分析:(Ⅰ)函数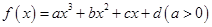 的零点的集合为
的零点的集合为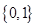 ,则方程
,则方程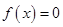 的解可以为
的解可以为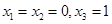 ,或
,或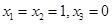 .
.
∴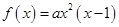 或
或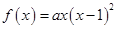 .
.
①若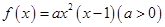 ,则
,则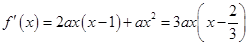 .
.
当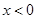 ,或
,或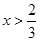 时,
时,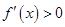 ,函数
,函数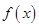 为增函数;当
为增函数;当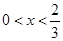 ,
,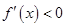 ,函数
,函数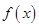 为减函数;
为减函数;
∴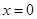 ,
,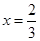 为函数的极值点.与题意不符.
为函数的极值点.与题意不符.
②若 ,则
,则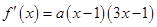
当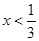 ,或
,或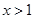 时,
时,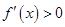 ,函数
,函数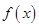 为增函数;当
为增函数;当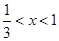 ,
,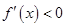 ,函数
,函数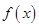 为减函数;
为减函数;
∴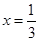 ,
,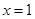 为函数的极值点.
为函数的极值点.
综上,函数 ,即
,即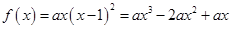 ,
,
而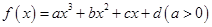 ,故
,故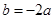 ,∴
,∴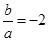 …6分
…6分
(Ⅱ)设过点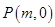 的直线与曲线
的直线与曲线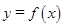 切于点
切于点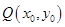 ,
,
由(Ⅰ)知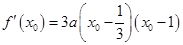 ,∴曲线
,∴曲线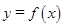 在点
在点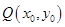 处的切线方程为
处的切线方程为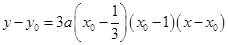 ,
,
∵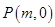 满足此方程,故
满足此方程,故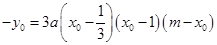 ,又
,又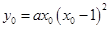
即 ,∴
,∴ .
.
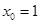 ,或
,或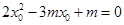 …①,关于
…①,关于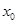 的方程
的方程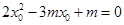 的判别式
的判别式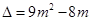
当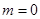 或
或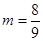 时,
时,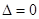 ,方程①有两等根
,方程①有两等根 或
或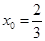 ,此时,过点
,此时,过点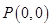 或
或 与曲线
与曲线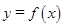 相切的直线有两条;
相切的直线有两条;
当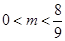 时,
时,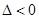 ,方程①无解,此时过点
,方程①无解,此时过点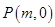 与曲线
与曲线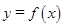 相切的直线仅有一条;
相切的直线仅有一条;
当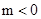 或
或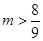 时,
时,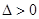 ,方程①有两个不同的实根,此时过点
,方程①有两个不同的实根,此时过点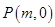 与曲线
与曲线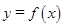 相切的直线有三条.
…12分
相切的直线有三条.
…12分
考点:函数的零点;函数的极值点;导数的几何意义;曲线的切线方程。
点评:利用导数求曲线的切线方程,我们一定要分清是“在某点处的切线”还是“过某点的切线”。对于“在某点处的切线”的问题,这一点就是切点,直接根据导数的几何意义写出切线方程即可。对于“过某点的切线”问题,我们一般要把切点坐标设出来解决。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目