题目内容
7.关于x的不等式ax2+2x-3a>0在x∈(1,3)恒成立,则实数a的取值范围是-1<a<1.分析 分类讨论,分离参数,确定函数的单调性,求最值,即可求出实数a的取值范围.
解答 解:x=$\sqrt{3}$时,恒成立;
x∈(1,$\sqrt{3}$)时,a<$\frac{-2x}{{x}^{2}-3}$,
令y=$\frac{-2x}{{x}^{2}-3}$,则y′=$\frac{-2(x+1)(x-3)}{({x}^{2}-3)^{2}}$,
∵x∈(1,$\sqrt{3}$),∴y′>0,
∴x∈(1,$\sqrt{3}$),函数单调递增,∴a<1;
x∈($\sqrt{3}$,3)时,a>$\frac{-2x}{{x}^{2}-3}$,
令y=$\frac{-2x}{{x}^{2}-3}$,则y′=$\frac{-2(x+1)(x-3)}{({x}^{2}-3)^{2}}$,
∵x∈($\sqrt{3}$,3),∴y′>0,
∴x∈($\sqrt{3}$,3),函数单调递增,∴a>-1,
综上所述,-1<a<1.
故答案为:-1<a<1.
点评 本题考查恒成立问题,考查导数知识的综合运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
18.在(ax6+$\frac{b}{x}$)4的二项展开式中,如果x3系数为20,那么ab3=( )
| A. | 20 | B. | 15 | C. | 10 | D. | 5 |
17. 在圆柱OO1中,ABCD为轴截面,AB=4,BC=6,D为⊙O1圆周上的点,$\widehat{BP}$的长度等于$\widehat{AP}$长度的2倍,则AD与PC所成角的余弦值为( )
在圆柱OO1中,ABCD为轴截面,AB=4,BC=6,D为⊙O1圆周上的点,$\widehat{BP}$的长度等于$\widehat{AP}$长度的2倍,则AD与PC所成角的余弦值为( )
 在圆柱OO1中,ABCD为轴截面,AB=4,BC=6,D为⊙O1圆周上的点,$\widehat{BP}$的长度等于$\widehat{AP}$长度的2倍,则AD与PC所成角的余弦值为( )
在圆柱OO1中,ABCD为轴截面,AB=4,BC=6,D为⊙O1圆周上的点,$\widehat{BP}$的长度等于$\widehat{AP}$长度的2倍,则AD与PC所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{3}$ |
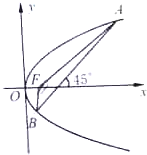 已知F是抛物线y2=8x的焦点,一条倾斜角为$\frac{π}{4}$的弦AB长为8$\sqrt{5}$(如图),求△FAB的面积和sin∠AFB的值.
已知F是抛物线y2=8x的焦点,一条倾斜角为$\frac{π}{4}$的弦AB长为8$\sqrt{5}$(如图),求△FAB的面积和sin∠AFB的值. 如图,从棱长为6cm的正方体铁皮箱ABCD-A1B1C1D1中分离出来由三个正方形面板组成的几何图形.
如图,从棱长为6cm的正方体铁皮箱ABCD-A1B1C1D1中分离出来由三个正方形面板组成的几何图形.