题目内容
(1)如果x(1-x)4+x2(1+2x)k+x3(1+3x)12展开式中x4的系数是144,求正整数k的值;
(2)求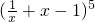 展开式中含x一次幂的项.
展开式中含x一次幂的项.
解:(1)x(1-x)4,x2(1+2x)k,x3(1+3x)12的展开式中x4的系数依次为-4,Ck2•22,C121•3,
据题应有-4+4Ck2+36=144,解得k=8.
(2)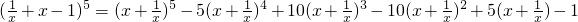 ,
,
分别计算各项中x项的系数,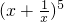 中通项
中通项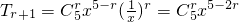 ,
,
r=2时得x项为T3=C52•x=10x;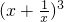 中通项为Tr+1=C3rx3-2r,r=1时得x项为 T2=C31x=3x,
中通项为Tr+1=C3rx3-2r,r=1时得x项为 T2=C31x=3x,
 中x项即为x;在
中x项即为x;在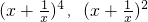 展开式中不含x项,故所求含x的项为10x+10•3x+5x=45x.
展开式中不含x项,故所求含x的项为10x+10•3x+5x=45x.
分析:(1)求出各式的展开式中x4的系数依次为-4,Ck2•22,C121•3,据题应有-4+4Ck2+36=144,解方程求的k值.
(2)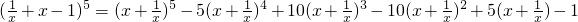 ,考查各个式子的通项,
,考查各个式子的通项,
求出各部分含x的项,求和即得结果.
点评:本题考查二项式系数的性质,二项式的展开式的通项公式,求出所有含x的项是解题的关键.
据题应有-4+4Ck2+36=144,解得k=8.
(2)
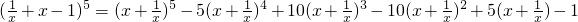 ,
,分别计算各项中x项的系数,
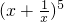 中通项
中通项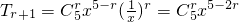 ,
,r=2时得x项为T3=C52•x=10x;
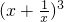 中通项为Tr+1=C3rx3-2r,r=1时得x项为 T2=C31x=3x,
中通项为Tr+1=C3rx3-2r,r=1时得x项为 T2=C31x=3x, 中x项即为x;在
中x项即为x;在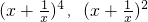 展开式中不含x项,故所求含x的项为10x+10•3x+5x=45x.
展开式中不含x项,故所求含x的项为10x+10•3x+5x=45x.分析:(1)求出各式的展开式中x4的系数依次为-4,Ck2•22,C121•3,据题应有-4+4Ck2+36=144,解方程求的k值.
(2)
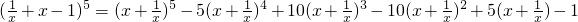 ,考查各个式子的通项,
,考查各个式子的通项,求出各部分含x的项,求和即得结果.
点评:本题考查二项式系数的性质,二项式的展开式的通项公式,求出所有含x的项是解题的关键.

练习册系列答案
相关题目