题目内容
18．若函数f（x）为偶函数，且在（0，∞）内是增函数，又f（-2015）=0，则不等式xf（x）＜0的解集是（ ）| A． | {x|x＜-2015或0＜x＜2015} | B． | {x|x＜-2015＜x＜0或x＞2015} | ||
| C． | {x|x＜-2015或x＞2015} | D． | {x|-2015＜x＜0或0＜x＜2015} |
分析 由条件可得到f（2015）=f（-2015）=0，f（x）在（-∞，0）内为减函数，从而解xf（x）＜0可得，$\left\{\begin{array}{l}{x＞0}\\{f（x）＜f（2015）}\end{array}\right.$，或$\left\{\begin{array}{l}{x＜0}\\{f（x）＞f（-2015）}\end{array}\right.$，从而根据f（x）的单调性即可得出原不等式的解集．
解答 解：根据题意，f（2015）=f（-2015）=0，f（x）在（-∞，0）内是减函数；
∴由xf（x）＜0得：
$\left\{\begin{array}{l}{x＞0}\\{f（x）＜0}\end{array}\right.$，或$\left\{\begin{array}{l}{x＜0}\\{f（x）＞0}\end{array}\right.$；
即$\left\{\begin{array}{l}{x＞0}\\{f（x）＜f（2015）}\end{array}\right.$，或$\left\{\begin{array}{l}{x＜0}\\{f（x）＞f（-2015）}\end{array}\right.$；
∴0＜x＜2015，或x＜-2015；
∴原不等式的解集为{x|x＜-2015，或0＜x＜2015}．
故选A．
点评 考查偶函数的定义，以及偶函数在对称区间上单调性的特点．
练习册系列答案
阅读快车系列答案
相关题目
9．芜湖市区甲、乙、丙三所学校的高三文科学生共有800人，其中男、女生人数如下表：
从这三所学校的所有高三文科学生中随机抽取1人，抽到乙校高三文科女生的概率为0.2．
（Ⅰ）求表中x+z的值；
（Ⅱ）钦州市五月份模考后，市教科所准备从这三所工作的所有高三文科学生中利用随机数表法抽取100人进行成绩统计分析，先将800人按001，002，…，800进行编号．如果从第8行第7列的数开始向右读，请你依次写出最先检测的3个人的编号；（下面摘取了随机数表中第7行至第9行）
8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 8392
6301 5316 5916 9275 3816 5821 7071 7512 8673 5807 4439
1326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931
（Ⅲ）已知x≥145，z≥145，求丙校高三文科生中的男生比女生人数多的概率．
| 甲校 | 乙校 | 丙校 | |
| 男生 | 97 | 90 | x |
| 女生 | 153 | y | z |
（Ⅰ）求表中x+z的值；
（Ⅱ）钦州市五月份模考后，市教科所准备从这三所工作的所有高三文科学生中利用随机数表法抽取100人进行成绩统计分析，先将800人按001，002，…，800进行编号．如果从第8行第7列的数开始向右读，请你依次写出最先检测的3个人的编号；（下面摘取了随机数表中第7行至第9行）
8442 1753 3157 2455 0688 7704 7447 6721 7633 5026 8392
6301 5316 5916 9275 3816 5821 7071 7512 8673 5807 4439
1326 3321 1342 7864 1607 8252 0744 3815 0324 4299 7931
（Ⅲ）已知x≥145，z≥145，求丙校高三文科生中的男生比女生人数多的概率．
6．函数$y=\frac{1}{{\sqrt{x+1}}}$的定义域是（ ）
| A． | （-1，+∞） | B． | [-1，+∞） | C． | （0，+∞） | D． | R |
13．数列{an}中，满足an+2=2an+1-an，且a1，a4031是函数f（x）=$\frac{1}{3}{x^3}-4{x^2}+6x-1$的极值点，则log2a2016的值是（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
10．
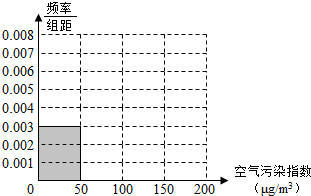空气污染，又称为大气污染，是指由于人类活动或自然过程引起某些物质进入大气中，呈现出足够的浓度，达到足够的时间，并因此危害了人体的舒适、健康和福利或环境的现象．全世界也越来越关注环境保护问题．当空气污染指数（单位：μg/m3）为0～50时，空气质量级别为一级，空气质量状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染；当空气污染指数为200～300时，空气质量级别为五级，空气质量状况属于重度污染；当空气污染指数为300以上时，空气质量级别为六级，空气质量状况属于严重污染．2015年8月某日某省x个监测点数据统计如下：
（Ⅰ）根据所给统计表和频率分布直方图中的信息求出x，y的值，并完成频率分布直方图；
（Ⅱ）在空气污染指数分别为50～100和150～200的监测点中，用分层抽样的方法抽取5个监测点，从中任意选取2个监测点，事件A“两个都为良”发生的概率是多少？
空气污染，又称为大气污染，是指由于人类活动或自然过程引起某些物质进入大气中，呈现出足够的浓度，达到足够的时间，并因此危害了人体的舒适、健康和福利或环境的现象．全世界也越来越关注环境保护问题．当空气污染指数（单位：μg/m3）为0～50时，空气质量级别为一级，空气质量状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染；当空气污染指数为200～300时，空气质量级别为五级，空气质量状况属于重度污染；当空气污染指数为300以上时，空气质量级别为六级，空气质量状况属于严重污染．2015年8月某日某省x个监测点数据统计如下：| 空气污染指数 （单位：μg/m3） | [0，50] | （50，100] | （100，150][ | （150，200] |
| 监测点个数 | 15 | 40 | y | 10 |
（Ⅱ）在空气污染指数分别为50～100和150～200的监测点中，用分层抽样的方法抽取5个监测点，从中任意选取2个监测点，事件A“两个都为良”发生的概率是多少？
7．在△ABC中，若$\sqrt{3}$（tanB+tanC）=tanBtanC-1，则sin2A=（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
8．若全集U={1，2，3，4}且∁UA={1}，则集合A的真子集共有（ ）
| A． | 3个 | B． | 5个 | C． | 7个 | D． | 8个 |