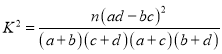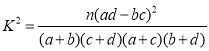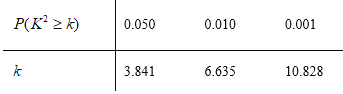题目内容
【题目】在3世纪中期,我国古代数学家刘徽在《九章算术注》中提出了割圆术:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆合体,而无所失矣”.这可视为中国古代极限观念的佳作.割圆术可以视为将一个圆内接正![]() 边形等分成
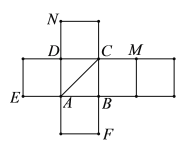
边形等分成![]() 个等腰三角形(如图所示),当
个等腰三角形(如图所示),当![]() 变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(
变得很大时,等腰三角形的面积之和近似等于圆的面积.运用割圆术的思想,可得到sin3°的近似值为( )(![]() 取近似值3.14)
取近似值3.14)
A.0.012B.0.052
C.0.125D.0.235
【答案】B
【解析】
根据题意圆内接正120边形其等分成120个等腰三角形,每个等腰三角形的顶角为![]() ,根据等腰三角形的面积之和近似等于圆的面积.即可列出等式解出sin3°的近似值.
,根据等腰三角形的面积之和近似等于圆的面积.即可列出等式解出sin3°的近似值.
当![]() 时,每个等腰三角形的顶角为
时,每个等腰三角形的顶角为![]() ,则其面积为
,则其面积为![]() ,
,
又因为等腰三角形的面积之和近似等于圆的面积,
所以![]() ,
,
故选:B

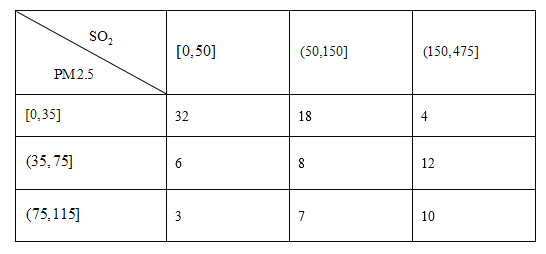
【题目】网络购物已经成为人们的一种生活方式.某购物平台为了给顾客提供更好的购物体验,为入驻商家设置了积分制度,每笔购物完成后,买家可以根据物流情况、商品质量等因素对商家做出评价,评价分为好评、中评和差评平台规定商家有50天的试营业时间,期间只评价不积分,正式营业后,每个好评给商家计1分,中评计0分,差评计![]() 分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
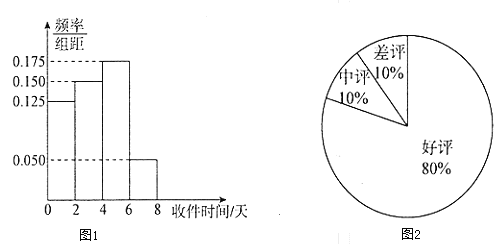
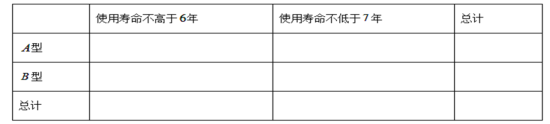
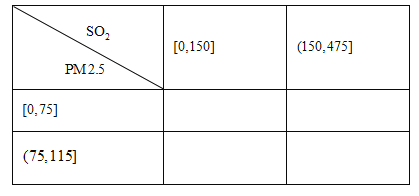
(1)通常收件时间不超过四天认为是物流迅速,否则认为是物流迟缓;
请根据题目所给信息完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“获得好评”与物流速度有关?
的把握认为“获得好评”与物流速度有关?
好评 | 中评或差评 | 合计 | |
物流迅速 | |||
物流迟缓 | 30 | ||
合计 |
(2)从正式营业开始,记商家在每笔交易中得到的评价得分为![]() .该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
.该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
表1
成交单数 | 36 | 30 | 27 |
天数 | 10 | 20 | 20 |
(Ⅰ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)平台规定,当积分超过10000分时,商家会获得“诚信商家”称号,请估计该商家从正式营业开始,1年内(365天)能否获得“诚信商家”称号
附: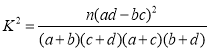
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |