题目内容
已知函数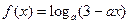 .
.
(1)当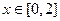 时
时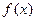 恒有意义,求实数
恒有意义,求实数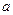 的取值范围.
的取值范围.
(2)是否存在这样的实数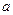 使得函数
使得函数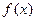 在区间[1,2]上为减函数,并且最大值为1,如果存在,试求出
在区间[1,2]上为减函数,并且最大值为1,如果存在,试求出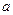 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
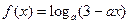 .
.(1)当
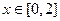 时
时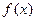 恒有意义,求实数
恒有意义,求实数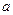 的取值范围.
的取值范围.(2)是否存在这样的实数
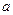 使得函数
使得函数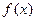 在区间[1,2]上为减函数,并且最大值为1,如果存在,试求出
在区间[1,2]上为减函数,并且最大值为1,如果存在,试求出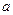 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.⑴(0,1)∪(1,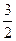 );⑵不存在。
);⑵不存在。
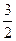 );⑵不存在。
);⑵不存在。解:(1)由假设,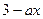 >0,对一切
>0,对一切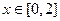 恒成立,
恒成立,
显然,函数g(x)=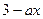 在[0,2]上为减函数,从而g(2)=
在[0,2]上为减函数,从而g(2)=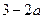 >0得到
>0得到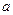 <
<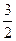
∴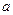 的取值范围是(0,1)∪(1,
的取值范围是(0,1)∪(1,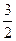 )
)
(2)假设存在这样的实数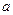 ,由题设知
,由题设知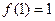 ,即
,即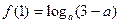 =1
=1
∴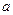 =
=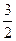 此时
此时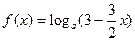
当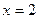 时,
时,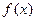 没有意义,故这样的实数不存在.
没有意义,故这样的实数不存在.
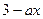 >0,对一切
>0,对一切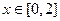 恒成立,
恒成立,
显然,函数g(x)=
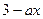 在[0,2]上为减函数,从而g(2)=
在[0,2]上为减函数,从而g(2)=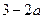 >0得到
>0得到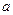 <
<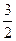
∴
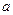 的取值范围是(0,1)∪(1,
的取值范围是(0,1)∪(1,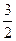 )
)(2)假设存在这样的实数
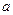 ,由题设知
,由题设知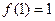 ,即
,即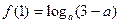 =1
=1∴
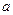 =
=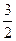 此时
此时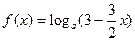
当
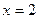 时,
时,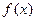 没有意义,故这样的实数不存在.
没有意义,故这样的实数不存在.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
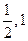 ) B、(1,0), C、(2,-1),则不能作为函数f(x)的解析式的是
) B、(1,0), C、(2,-1),则不能作为函数f(x)的解析式的是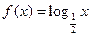 B.
B.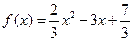
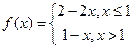 D.
D.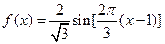
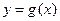 的图象如下图所示,则函数
的图象如下图所示,则函数 的图象大致是
的图象大致是
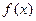 的全体:若存在非零常数k,对任意
的全体:若存在非零常数k,对任意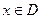 ,等式
,等式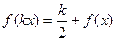 恒成立。(Ⅰ)判断一次函数
恒成立。(Ⅰ)判断一次函数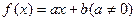 是否属于集合M;(Ⅱ)证明
是否属于集合M;(Ⅱ)证明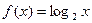 属于集合M,并找到一个常数k;(Ⅲ)已知函数
属于集合M,并找到一个常数k;(Ⅲ)已知函数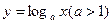 与
与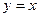 的图像有公共点,试证明
的图像有公共点,试证明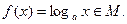
 ,则 ( )
,则 ( ) __________。
__________。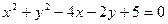 ,则
,则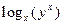 的值是_____________.
的值是_____________.