题目内容
已知函数f(x)=loga[
-(2a)x]对任意x∈[
,+∞)都有意义,则实数a的取值范围是( )
| x |
| 1 |
| 2 |
A.(0,
| B.(0,
| C.[
| D.(
|
要使f(x)=loga[
-(2a)x]对任意x∈[
,+∞)都有意义,
则对任意x∈[
,+∞),有
>(2a)x恒成立,
显然0<2a<1,否则,在x∈[
,+∞)时,一定存在x=x0,当x>x0时,有
<(2a)x.
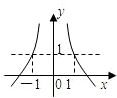
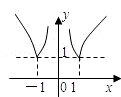
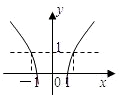
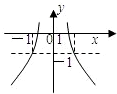
令g(x)=(2a)x,h(x)=
,
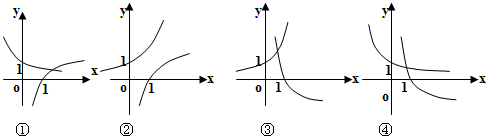
如图:

由图可知,在x=
处的函数g(x)=(2a)x的值小于h(x)=
的值,
∴
<
,
∴a<
.
又a>0且a≠1.
∴0<a<
.
则实数a的取值范围是(0,
).
故选:B.
| x |
| 1 |
| 2 |
则对任意x∈[
| 1 |
| 2 |
| x |
显然0<2a<1,否则,在x∈[
| 1 |
| 2 |
| x |
令g(x)=(2a)x,h(x)=
| x |
如图:

由图可知,在x=
| 1 |
| 2 |
| x |
∴
| 2a |
| ||
| 2 |
∴a<
| 1 |
| 4 |
又a>0且a≠1.
∴0<a<
| 1 |
| 4 |
则实数a的取值范围是(0,
| 1 |
| 4 |
故选:B.

练习册系列答案
相关题目
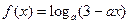 .
.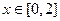 时
时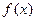 恒有意义,求实数
恒有意义,求实数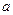 的取值范围.
的取值范围.