题目内容
下列命题中,真命题的个数为( )
(1)在△ABC中,若A>B,则sinA>sinB;
(2)已知
=(3,4),
=(-2,-1),则
在
上的投影为-2;
(3)已知p:?x∈R,cosx=1,q:?x∈R,x2-x+1>0,则“p∧¬q”为假命题;
(4)函数f(x)=xsinx在(0,π)上有最大值,没有最小值.
(1)在△ABC中,若A>B,则sinA>sinB;
(2)已知
| AB |
| CD |
| AB |
| CD |
(3)已知p:?x∈R,cosx=1,q:?x∈R,x2-x+1>0,则“p∧¬q”为假命题;
(4)函数f(x)=xsinx在(0,π)上有最大值,没有最小值.
分析:根据正弦定理及三角形中“大边对大角”,可以判断(1)的真假;
根据向量投影的定义,计算出
在
上的投影,可判断(2)的真假;
根据余弦函数和二次函数的图象和性质,分别判断命题p,q的真假,进而根据复合命题真假判断的真值表得到答案.
利用导数法,求出函数的导数,分析其最值是否存在,可判断(4)的真假,进而得到答案.
根据向量投影的定义,计算出
| AB |
| CD |
根据余弦函数和二次函数的图象和性质,分别判断命题p,q的真假,进而根据复合命题真假判断的真值表得到答案.
利用导数法,求出函数的导数,分析其最值是否存在,可判断(4)的真假,进而得到答案.
解答:解:在△ABC中,若A>B⇒a>b⇒2rsinA>2rsinB⇒sinA>sinB,故(1)正确;
∵
=(3,4),
=(-2,-1),则
在
上的投影为
=
=-2
,故(2)不正确;
∵x=0时,cosx=1,故命题p为真命题,
∵y=x2-x+1的图象开口朝上,且与x轴没有交点,故命题q为真命题,故“p∧¬q”为假命题,故(3)正确.
∵f(x)=xsinx,故f′(x)=sinx+xcosx,
令f′(x)=0,则x=-tanx,
∵存在x0∈(0,π)使x=-tanx,故当x=x0时,函数f(x)=xsinx取最大值,但没有最小值,故(4)正确
故真命题有3个,
故选C
∵
| AB |
| CD |
| AB |
| CD |
| ||||
|
|
| -10 | ||
|
| 5 |
∵x=0时,cosx=1,故命题p为真命题,
∵y=x2-x+1的图象开口朝上,且与x轴没有交点,故命题q为真命题,故“p∧¬q”为假命题,故(3)正确.
∵f(x)=xsinx,故f′(x)=sinx+xcosx,
令f′(x)=0,则x=-tanx,
∵存在x0∈(0,π)使x=-tanx,故当x=x0时,函数f(x)=xsinx取最大值,但没有最小值,故(4)正确
故真命题有3个,
故选C
点评:本题以命题的真假判断为载体考查了正弦定理,向量的投影,对数函数的图象和性质,正弦型函数的图象和性质,其中(3)(4)较难

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
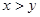 ,则
,则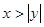 ”的逆命题
”的逆命题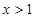 ,则
,则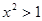 ”的否命题
”的否命题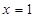 ,则
,则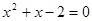 ”的否命题
”的否命题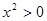 ,则
,则