题目内容
已知命题p：方程mx2+4y2=4m（m∈R）表示焦点在y轴上的椭圆，命题q：?x∈R，cosx-m＞0恒成立．若p∨q为假命题，则实数m的取值范围是______．
方程mx2+4y2=4m（m∈R）表示焦点在y轴上的椭圆，
则m≠0，椭圆的标准方程为
+
=1，
则m＞4．
即命题p真时，m＞4，则p假时，m≤4；
若?x∈R，cosx-m＞0恒成立，
则m＜cosx，∴m＜-1，
命题q真时，m＜-1，命题q假时，m≥-1，
若p∨q为假命题，则p假q假，
即
，即-1≤m≤4．
故实数m的取值范围是-1≤m≤4．
故答案为：-1≤m≤4．
则m≠0，椭圆的标准方程为
| x2 |
| 4 |
| y2 |
| m |
则m＞4．
即命题p真时，m＞4，则p假时，m≤4；
若?x∈R，cosx-m＞0恒成立，
则m＜cosx，∴m＜-1，
命题q真时，m＜-1，命题q假时，m≥-1，
若p∨q为假命题，则p假q假，
即
|
故实数m的取值范围是-1≤m≤4．
故答案为：-1≤m≤4．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
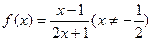的对称中心是
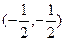；③对任意实数a,b则
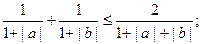④取一根长为3m的绳子，拉直后在任意位置剪断，那么剪得两段的长度都不少于1m的概率是
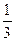；⑤如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值，则△A1B1C1为锐角三角形，△A2B2C2为钝角三角形.其中真命题的序号是 （将所有真命题的序号都填上）.