题目内容
设f(x)是定义在[-1,1]上的偶函数,g(x)与f(x)的图象关于直线x=1对称,当x∈[2,3]时,g(x)=2t(x-2)-4(x-2)3(t为常数).
(1)求f(x)的表达式.
(2)当t∈![]() 时,求f(x)在[0,1]上取最大值时对应的x值;猜想f(x)在[0,1]上的单调增区间,给予证明.
时,求f(x)在[0,1]上取最大值时对应的x值;猜想f(x)在[0,1]上的单调增区间,给予证明.
(3)当t>6时,是否存在t使f(x)的图象的最高点落在直线y=12上?若存在,求t的值;若不存在说明理由.
答案:
解析:
解析:
|
设P(x0,y0)是y=f(x)图象上任一点,则y0=f(x0),P关于x=1的对称点 又∵ f(x)=g(2-x),设x∈[-1,0],则2-x∈[2,3] f(x)=g(2-x)=-2tx+4x3,x∈[-1,0] 又∵f(x)为偶函数,当x∈[0,1],f(x)=f(-x)=2tx-4x3 ∴f(x)= ②t∈[2,6],x∈[0,1],f(x)=2tx-4x3 当0≤x< ∴当x= ③f(x)为偶函数,只讨论x∈[0,1]情形t>6时, f(x)最大值=f(1)=2t-4=12.t=8.存在t=8. |

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
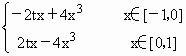
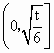
 >0.
>0. )<f(x-
)<f(x- );
); ∈(O,1),
∈(O,1), ,若f(
,若f( )≥f(
)≥f(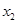 ),则(0,
),则(0, f(
f( 为含峰区间:
为含峰区间: ,使得由(I)所确定的含峰区间的长度不大于0.5+r:
,使得由(I)所确定的含峰区间的长度不大于0.5+r: 或
或 ,在所得的含峰区间内选取
,在所得的含峰区间内选取 ,由
,由 ,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)
,满足两两之差的绝对值不小于0.02,且使得新的含峰区间的长度缩短到0. 34(区间长度等于区间的右端点与左端点之差)