题目内容
【题目】如图，抛物线y=ax2+2x+c经过点A（0，3），B（﹣1，0），抛物线的顶点为点D，对称轴与x轴交于点E，连结BD，则抛物线表达式：BD的长为 ．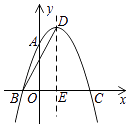 
【答案】y=﹣x2+2x+3；2 
【解析】解：由抛物线的性质可知：抛物线y=ax2+2x+c经过点A（0，3），即c=3， ∴抛物线y=ax2+2x+3经过点B（﹣1，0），代入求得a=﹣1，
∴抛物线的表达式y=﹣x2+2x+3，
由y=﹣x2+2x+3=﹣（x﹣1）2+4，
∴抛物线的顶点为点D（1，4），
由两点之间的距离公式|BD|= 
=2 ，
|BD|=2 ，
所以答案是：y=﹣x2+2x+3，2 ．
【考点精析】掌握二次函数的性质是解答本题的根本，需要知道当
时，抛物线开口向上，函数在
上递减，在
上递增；当
时，抛物线开口向下，函数在上递增，在上递减．
名校课堂系列答案
【题目】某企业为了对生产的一种新产品进行合理定价，将该产品按事先拟定的价格进行试销，得到以下数据：
单价x（元/件） | 60 | 62 | 64 | 66 | 68 | 70 |
销量y（件） | 91 | 84 | 81 | 75 | 70 | 67 |
（I）画出散点图，并求
关于
的回归方程；
（II）已知该产品的成本是36元/件，预计在今后的销售中，销量与单价仍然服从（I）中的关系，为使企业获得最大利润，该产品的单价应定为多少元（精确到元）？
附：回归直线
的斜率和截距的最小二乘法估计公式分别为：
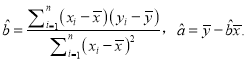
【题目】全世界越来越关注环境保护问题，某监测站点于2016年8月某日起连续
天监测空气质量指数
，数据统计如下：
空气质量指数 |
|
|
|
|
|
空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
天数 |
|
|
|
|
|
（1）根据所给统计表和频率分布直方图中的信息求出
的值，并完成頻率分布直方图：
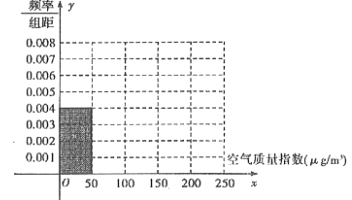
（2）由頻率分布直方图，求该组数据的平均数与中位数；
（3）在空气质量指数分别为
和
的监测数据中，用分层抽样的方法抽取
天，从中任意选取
天，求事件
“两天空气都为良”发生的概率.