题目内容
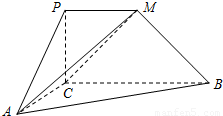
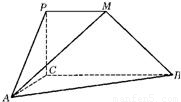
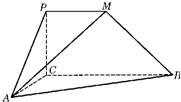 如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°.
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°.(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的大小;
(Ⅲ)求多面体PMABC的体积.
分析:(Ⅰ)要证AC⊥BM,只要证明AC⊥平面PCBM中的两条相交直线即可.
(Ⅱ)求二面角M-AB-C的大小,用三垂线定理,作出二面角的平面角,求解即可;
也可以利用空间直角坐标系来解.
(Ⅲ)求多面体PMABC的体积,找出底面,求出底面面积,求出高,即可解答.
(Ⅱ)求二面角M-AB-C的大小,用三垂线定理,作出二面角的平面角,求解即可;
也可以利用空间直角坐标系来解.
(Ⅲ)求多面体PMABC的体积,找出底面,求出底面面积,求出高,即可解答.
解答: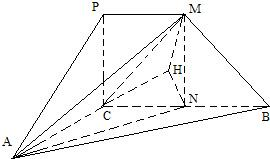 解:(Ⅰ)∵平面PCBM⊥平面ABC,AC⊥BC,AC?平面ABC,
解:(Ⅰ)∵平面PCBM⊥平面ABC,AC⊥BC,AC?平面ABC,
∴AC⊥平面PCBM.
又∵BM?平面PCBM,
∴AC⊥BM.
(Ⅱ)取BC的中点N,则CN=1.连接AN、MN.
∵平面PCBM⊥平面ABC,平面PCBM∩平面ABC=BC,PC⊥BC.
∴PC⊥平面ABC.
∵PM∥CN,∴MN∥PC,从而MN⊥平面ABC.
作NH⊥AB于H,连接MH,则由三垂线定理知AB⊥MH.
从而∠MHN为二面角M-AB-C的平面角.
∵直线AM与直线PC所成的角为60°,
∴∠AMN=60°.
在△ACN中,由勾股定理得AN=
.
在Rt△AMN中,MN=AN•cot∠AMN=
•
=
.
在Rt△BNH中,NH=BN•sin∠ABC=BN•
=1×
=
.
在Rt△MNH中,tan∠MHN=
=
=
故二面角M-AB-C的大小为arctan
.
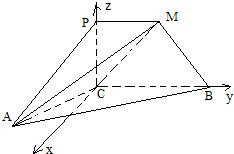 (Ⅱ)如图以C为原点建立空间直角坐标系C-xyz.
(Ⅱ)如图以C为原点建立空间直角坐标系C-xyz.
设P(0,0,z0)(z0>0),有B(0,2,0),A(1,0,0),M(0,1,z0).
=(-1,1,z0),
=(0,0,z0)
由直线AM与直线PC所成的角为60°,得
•
=|
|•|
|•cos60°
即
=
•z0,解得z0=
.
∴
=(-1,1,
),
=(-1,2,0)
设平面MAB的一个法向量为
=(x1,y1,z1),则
由
?
,取z1=
,得
=(4,2,
)
取平面ABC的一个法向量为
=(0,0,1)
则cos<
,
>=
=
=
由图知二面角M-AB-C为锐二面角,
故二面角M-AB-C的大小为arccos
.
(Ⅲ)多面体PMABC就是四棱锥A-BCPMVPMABC=VA-PMBC=
•SPMBC•AC=
•
•(PM+CB)•CP•AC=
•
•(2+1)•
•1=
.
 解:(Ⅰ)∵平面PCBM⊥平面ABC,AC⊥BC,AC?平面ABC,
解:(Ⅰ)∵平面PCBM⊥平面ABC,AC⊥BC,AC?平面ABC,∴AC⊥平面PCBM.
又∵BM?平面PCBM,
∴AC⊥BM.
(Ⅱ)取BC的中点N,则CN=1.连接AN、MN.
∵平面PCBM⊥平面ABC,平面PCBM∩平面ABC=BC,PC⊥BC.
∴PC⊥平面ABC.
∵PM∥CN,∴MN∥PC,从而MN⊥平面ABC.
作NH⊥AB于H,连接MH,则由三垂线定理知AB⊥MH.
从而∠MHN为二面角M-AB-C的平面角.
∵直线AM与直线PC所成的角为60°,
∴∠AMN=60°.
在△ACN中,由勾股定理得AN=
| 2 |
在Rt△AMN中,MN=AN•cot∠AMN=
| 2 |
| ||
| 3 |
| ||
| 3 |
在Rt△BNH中,NH=BN•sin∠ABC=BN•
| AC |
| AB |
| 1 | ||
|
| ||
| 5 |
在Rt△MNH中,tan∠MHN=
| MN |
| NH |
| ||||
|
| ||
| 3 |
故二面角M-AB-C的大小为arctan
| ||
| 3 |
 (Ⅱ)如图以C为原点建立空间直角坐标系C-xyz.
(Ⅱ)如图以C为原点建立空间直角坐标系C-xyz.设P(0,0,z0)(z0>0),有B(0,2,0),A(1,0,0),M(0,1,z0).
| AM |
| CP |
由直线AM与直线PC所成的角为60°,得
| AM |
| CP |
| AM |
| CP |
即
| z | 2 0 |
| 1 |
| 2 |
|
| ||
| 3 |
∴
| AM |
| ||
| 3 |
| AB |
设平面MAB的一个法向量为
| n1 |
由
|
|
| 6 |
| n1 |
| 6 |
取平面ABC的一个法向量为
| n2 |
则cos<
| n1 |
| n2 |
| ||||
|
|
| ||
|
| ||
| 13 |
由图知二面角M-AB-C为锐二面角,
故二面角M-AB-C的大小为arccos
| ||
| 13 |
(Ⅲ)多面体PMABC就是四棱锥A-BCPMVPMABC=VA-PMBC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
点评:本题主要考查异面直线所成的角、平面与平面垂直、二面角、棱锥体积等有关知识,
考查思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力.
考查思维能力和空间想象能力、应用向量知识解决数学问题的能力、化归转化能力和推理运算能力.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
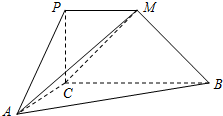 如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,已知AC=PC=PM=1,BC=2,∠ACB=90°.
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,已知AC=PC=PM=1,BC=2,∠ACB=90°.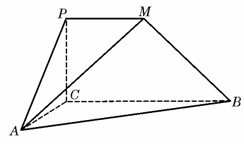 (2)求二面角M-AB-C的余弦值
(2)求二面角M-AB-C的余弦值