题目内容
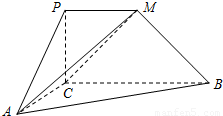
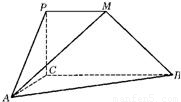
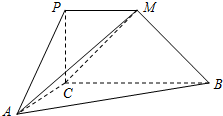 如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,已知AC=PC=PM=1,BC=2,∠ACB=90°.
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,已知AC=PC=PM=1,BC=2,∠ACB=90°.(1)求证:AC⊥BM;
(2)求证:平面ABM⊥平面ACM;
(3)求二面角M-AC-B的大小.
分析:(1)由平面PCBN⊥平面ABC,AC⊥BC,知AC⊥平面PCBM,由此能够证明AC⊥BM.
(2)取BC的中点N,则CN=1,连接AN,MN,则由已知,△CNB和△BNM均为等腰直角三角形,故∠CMN=∠BMN=45°,∠CMB=90°,∠CMN=∠BMN=45°,所以CM⊥BM,由此能够证明平面ABM⊥平面ACM.
(3)由(1)知,AC⊥平面PCBM,又因为AC⊥CM,所以∠MCB为二面角M-AC-B的平面角,由此能够求出二面角M-AC-B的大小.
(2)取BC的中点N,则CN=1,连接AN,MN,则由已知,△CNB和△BNM均为等腰直角三角形,故∠CMN=∠BMN=45°,∠CMB=90°,∠CMN=∠BMN=45°,所以CM⊥BM,由此能够证明平面ABM⊥平面ACM.
(3)由(1)知,AC⊥平面PCBM,又因为AC⊥CM,所以∠MCB为二面角M-AC-B的平面角,由此能够求出二面角M-AC-B的大小.
解答:解:(1)∵平面PCBN⊥平面ABC,AC⊥BC,AC?平面ABC,
∴AC⊥平面PCBM,
又∵BM?平面PCBM,
∴AC⊥BM.
(2)取BC的中点N,则CN=1,
连接AN,MN,则由已知,△CNB和△BNM均为等腰直角三角形,
∴∠CMN=∠BMN=45°,
∴∠CMB=90°,
∴∠CMN=∠BMN=45°,
∴∠CMB=90°,
∴CM⊥BM,
由(1)AC⊥BM,∴BM⊥平面ACM,
又∵BM?平面ABM,∴平面ABM⊥平面ACM.
(3)由(1)知,AC⊥平面PCBM,
又∵CM?平面PCBM,∴AC⊥CM,
∴∠MCB为二面角M-AC-B的平面角,
∵∠MCB=45°,
∴二面角M-AC-B的大小为45°.
∴AC⊥平面PCBM,
又∵BM?平面PCBM,
∴AC⊥BM.
(2)取BC的中点N,则CN=1,
连接AN,MN,则由已知,△CNB和△BNM均为等腰直角三角形,
∴∠CMN=∠BMN=45°,
∴∠CMB=90°,
∴∠CMN=∠BMN=45°,
∴∠CMB=90°,
∴CM⊥BM,
由(1)AC⊥BM,∴BM⊥平面ACM,
又∵BM?平面ABM,∴平面ABM⊥平面ACM.
(3)由(1)知,AC⊥平面PCBM,
又∵CM?平面PCBM,∴AC⊥CM,
∴∠MCB为二面角M-AC-B的平面角,
∵∠MCB=45°,
∴二面角M-AC-B的大小为45°.
点评:本题考查直线与直线垂直的证明,考查平面与平面垂直的证明,考查二面角的求法.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
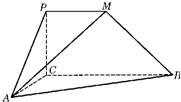 如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°.
如图,平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2PM=2,∠ACB=90°.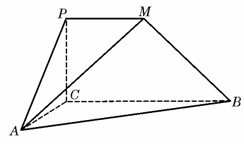 (2)求二面角M-AB-C的余弦值
(2)求二面角M-AB-C的余弦值