题目内容
 设b>0,椭圆方程为
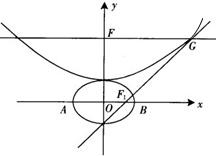
设b>0,椭圆方程为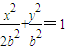 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点,试探究在抛物线上是否存在点P,使得△ABP为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
【答案】分析:(1)先求出G点的坐标,利用导数求出过点G的切线斜率,得到过点G的切线方程,根据由切线方程求得的F1点的坐标,与用椭圆方程得F1点的坐标应该相同,求出b,椭圆和抛物线的方程可得.
(2)以∠PAB为直角的Rt△ABP只有一个,以∠PBA为直角的Rt△ABP只有一个,以AB为直径的圆与抛物线有两个交点,根据直径对的圆周角等于直角,以∠APB为直角的Rt△ABP有两个.所以,共得到4个直角三角形.
解答:解:(1)由x2=8(y-b)得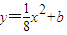 ,
,
当y=b+2得x=±4,∴G点的坐标为(4,b+2),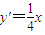 ,y'|x=4=1,
,y'|x=4=1,
过点G的切线方程为y-(b+2)=x-4即y=x+b-2,
令y=0得x=2-b,∴F1点的坐标为(2-b,0),由椭圆方程得F1点的坐标为(b,0),
∴2-b=b即b=1,即椭圆和抛物线的方程分别为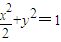 和x2=8(y-1);(7分)
和x2=8(y-1);(7分)
(2)∵过A作x轴的垂线与抛物线只有一个交点P,∴以∠PAB为直角的Rt△ABP只有一个,
同理∴以∠PBA为直角的Rt△ABP只有一个;
若以∠APB为直角,则点P在以AB为直径的圆上,而以AB为直径的圆与抛物线有两个交点.
所以,以∠APB为直角的Rt△ABP有两个;
因此抛物线上存在四个点使得△ABP为直角三角形.(15分)
点评:本题考查利用导数求切线的斜率,待定系数法求椭圆和抛物线的方程,体现了分类讨论的数学思想.
(2)以∠PAB为直角的Rt△ABP只有一个,以∠PBA为直角的Rt△ABP只有一个,以AB为直径的圆与抛物线有两个交点,根据直径对的圆周角等于直角,以∠APB为直角的Rt△ABP有两个.所以,共得到4个直角三角形.
解答:解:(1)由x2=8(y-b)得
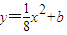 ,
,当y=b+2得x=±4,∴G点的坐标为(4,b+2),
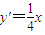 ,y'|x=4=1,
,y'|x=4=1,过点G的切线方程为y-(b+2)=x-4即y=x+b-2,
令y=0得x=2-b,∴F1点的坐标为(2-b,0),由椭圆方程得F1点的坐标为(b,0),
∴2-b=b即b=1,即椭圆和抛物线的方程分别为
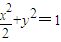 和x2=8(y-1);(7分)
和x2=8(y-1);(7分)(2)∵过A作x轴的垂线与抛物线只有一个交点P,∴以∠PAB为直角的Rt△ABP只有一个,
同理∴以∠PBA为直角的Rt△ABP只有一个;
若以∠APB为直角,则点P在以AB为直径的圆上,而以AB为直径的圆与抛物线有两个交点.
所以,以∠APB为直角的Rt△ABP有两个;
因此抛物线上存在四个点使得△ABP为直角三角形.(15分)
点评:本题考查利用导数求切线的斜率,待定系数法求椭圆和抛物线的方程,体现了分类讨论的数学思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 设b>0,椭圆方程为
设b>0,椭圆方程为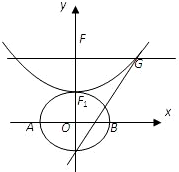 设b>0,椭圆方程为
设b>0,椭圆方程为 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为 设b>0,椭圆方程为
设b>0,椭圆方程为 ,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.
,抛物线方程为x2=8(y-b).如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的交点为G,已知抛物线在点G的切线经过椭圆的右焦点F1.