题目内容
(本小题满分12分)
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC ,AB=2,已知AE与平面ABC所成的角为θ,且tanθ=。
(Ⅰ)证明:平面ACD⊥平面ADE;
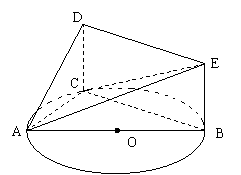 (Ⅱ)记AC=x,V(x)表示三棱锥A-CBE的体积,求V(x)的表达式;
(Ⅱ)记AC=x,V(x)表示三棱锥A-CBE的体积,求V(x)的表达式;
(Ⅲ)当V(x)取得最大值时,求二面角D-AB-C的大小。
(Ⅰ)证明:∵四边形DCBE为平行四边形 ∴CD∥BE,BC∥DE
∵ DC⊥平面ABC ,BCÌ平面ABC ∴DC⊥BC.
∵AB是圆O的直径 ∴BC⊥AC且DC∩AC=C ∴BC⊥平面ADC.
∵DE//BC ∴DE⊥平面ADC
又∵DEÌ平面ADE ∴平面ACD⊥平面![]() ………………3分
………………3分
(Ⅱ)∵ DC![]() 平面ABC ∴
平面ABC ∴![]() 平面ABC
平面ABC
∴![]() 为AE与平面ABC所成的角,即
为AE与平面ABC所成的角,即![]() =
=![]()
在Rt△ABE中,由![]() ,
,![]() 得
得![]()
在Rt△ABC中 ∵![]() (
(![]() )
)
∴![]()
∴![]()
![]() (
(![]() )---7分
)---7分
(Ⅲ)由(Ⅱ)知![]()
要![]() 取得最大值,当且仅当
取得最大值,当且仅当![]() 取得最大值,
取得最大值,![]()
∵![]() 当且仅当
当且仅当![]() ,即
,即![]() 时,“=”成立,
时,“=”成立,
∴当![]() 取得最大值时
取得最大值时![]() ,这时△ACB为等腰直角三角形--9分
,这时△ACB为等腰直角三角形--9分
 连结CO,DO
连结CO,DO
∵AC=BC,DC=DC
∴![]() ≌
≌![]() ∴AD=DB
∴AD=DB
又∵O为AB的中点 ∴![]()
∴![]() 为二面角D-AB-C的平面角
为二面角D-AB-C的平面角
在![]() 中 ∵
中 ∵![]() ,
,![]()
∴![]() , ∴
, ∴![]() =
=![]()
即当![]() 取得最大值时,二面角D-AB-C为60°.------12分
取得最大值时,二面角D-AB-C为60°.------12分

练习册系列答案
相关题目