题目内容
已知二面角α-l-β为直二面角，A是α内一定点，过A作直线AB交β于B，若直线AB与二面角α-l-β的两个半平面α，β所成的角分别为30°和60°，则这样的直线最多有（ ）
分析：由已知中二面角α-l-β为直二面角，A是α内一定点，过A作直线AB交β于B，若直线AB与二面角α-l-β的两个半平面α，β所成的角分别为30°和60°，我们过A点做AC⊥l，交点为C，连接BC后，易证得l⊥平面ABC，则B点的位置被唯一确定，进而得到答案．
解答：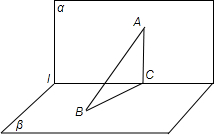
解：过A点向l做垂直，垂足为C，连接BC，如图所示：
∵二面角α-l-β为直二面角，
∴∠ACB=90°，∠ABC即为l与β所成的角，即∠ABC=60°，
则∠BAC=30°即，∠BAC即为l与α所成的角，
则BC⊥l，由AC∩BC=C
则l⊥平面ABC
故满足条件的B点只有一个
故选A
解：过A点向l做垂直，垂足为C，连接BC，如图所示：∵二面角α-l-β为直二面角，
∴∠ACB=90°，∠ABC即为l与β所成的角，即∠ABC=60°，
则∠BAC=30°即，∠BAC即为l与α所成的角，
则BC⊥l，由AC∩BC=C
则l⊥平面ABC
故满足条件的B点只有一个
故选A
点评：本题考查的知识点是平面的基本性质及推论，其中添加辅助线，利用数形结合的思想，借助图形的直观性，分析答案是解答本题的关键．
练习册系列答案
相关题目
已知二面角α-l-β的大小为60°，b和c是两条直线，则下列四个条件中，一定能使b和c所成的角为60°的条件是（ ）
| A、b∥α，c∥β | B、b∥α，c⊥β | C、b⊥α，c⊥β | D、b⊥α，c∥β |