题目内容
【题目】在正方形SG1G2G3中,E、F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE、SF及EF把这个正方形折成一个四面体,使G1、G2、G3三点重合,重合后的点记为G,那么,在四面体S﹣EFG中必有( )
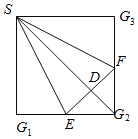
A.SG⊥△EFG所在平面B.SD⊥△EFG所在平面
C.GF⊥△SEF所在平面D.GD⊥△SEF所在平面
【答案】A
【解析】
在正方形SG1G2G3中,有S G1⊥G1E,在折叠后其垂直关系不变,所以有SG⊥EG.同理有有SG⊥FG,再由线面垂直的判定定理证明.
在正方形SG1G2G3中,
因为S G1⊥G1E,
所以在四面体中有SG⊥EG.
又因为S G3⊥G3F,
所以在四面体中有SG⊥FG,且![]() ,
,
所以 SG⊥△EFG所在平面.
故选:A

练习册系列答案
相关题目