题目内容
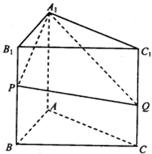 如图,三棱柱ABC-A1B1C1,侧棱与底面垂直,AB=AC=1,AA1=2,P、Q、M分别是棱BB1、CC1、B1C1的中点,AB⊥AQ.
如图,三棱柱ABC-A1B1C1,侧棱与底面垂直,AB=AC=1,AA1=2,P、Q、M分别是棱BB1、CC1、B1C1的中点,AB⊥AQ.(1)求证:AC⊥A1P;
(2)求证:AQ∥面A1PM;
(3)求AQ与面BCC1B1所成角的大小.
分析:(1)要证AC⊥A1P只需证明AC垂直A1P所在的平面AA1B1B即可,只需证明垂直平面AA1B1B内的两条相交直线AB,AA1,即可.
(2)延长线PM交CC1于J,证明AQ平行面A1PM内的直线A1J,就证明AQ∥面A1PM;
(3)说明∠A1JM就是AQ与面BCC1B1所成角,解三角形A1JM,求AQ与面BCC1B1所成角的大小.
(2)延长线PM交CC1于J,证明AQ平行面A1PM内的直线A1J,就证明AQ∥面A1PM;
(3)说明∠A1JM就是AQ与面BCC1B1所成角,解三角形A1JM,求AQ与面BCC1B1所成角的大小.
解答:解:(1)由已知AA1⊥AB,又AB⊥A1Q,
∵AB⊥面AA1C1C,
∴AB⊥AC,
又∵AC⊥AA1,
∴AC⊥面AA1B1B,
∴AC⊥A1P(5分)
(2)延长线PM交CC1于J.
∵P,M是棱B1B,B1C1中点,
∴△B1PM≌△C1MJ,
∴C1J=1.
在面AA1C1C中由AA1∥QJ,
∵CQ=1,
∴AA1=QJ.
∴四边形A1AQJ是平行四边形.
∴AQ∥A1J,
∴AQ∥面A1PM.(10分)
(3)M是等腰三角形A1B1C1中点,A1M⊥B1C1,
又由已知A1M⊥CC1,∴A1M⊥面BCB1C1,又A1J∥AQ,
∴∠A1JM就是AQ与面BCC1B1所成角.
A1M=
,A1J=
,∴sin∠A1JM=
,∴∠A1JM=30°
即AQ与面BCC1B1所成角为30°(14分)
∵AB⊥面AA1C1C,
∴AB⊥AC,
又∵AC⊥AA1,
∴AC⊥面AA1B1B,
∴AC⊥A1P(5分)
(2)延长线PM交CC1于J.
∵P,M是棱B1B,B1C1中点,
∴△B1PM≌△C1MJ,
∴C1J=1.
在面AA1C1C中由AA1∥QJ,
∵CQ=1,
∴AA1=QJ.
∴四边形A1AQJ是平行四边形.
∴AQ∥A1J,
∴AQ∥面A1PM.(10分)
(3)M是等腰三角形A1B1C1中点,A1M⊥B1C1,
又由已知A1M⊥CC1,∴A1M⊥面BCB1C1,又A1J∥AQ,
∴∠A1JM就是AQ与面BCC1B1所成角.
A1M=
| ||
| 2 |
| 2 |
| 1 |
| 2 |
即AQ与面BCC1B1所成角为30°(14分)
点评:本题考查直线与平面平行的判定,直线与平面所成的角,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
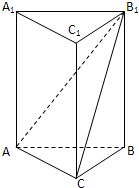
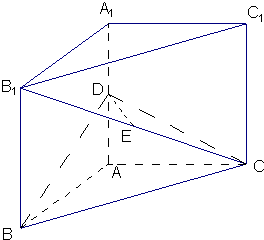 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.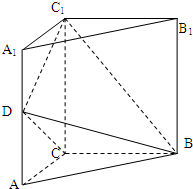 (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=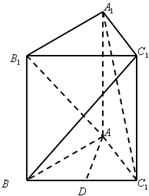 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB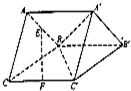 (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=