题目内容
已知函数f(x)=ln(ex+a)(a为常数)是实数集R上的奇函数.
(Ⅰ)求实数a的值;
(Ⅱ)讨论关于x的方程lnx=f(x)(x2-2ex+m)的根的个数.
(Ⅲ)证明:
+
+…+
<
(n∈N*,n≥2).
(Ⅰ)求实数a的值;
(Ⅱ)讨论关于x的方程lnx=f(x)(x2-2ex+m)的根的个数.
(Ⅲ)证明:
| ln(22-1) |
| 22 |
| ln(32-1) |
| 32 |
| ln(n2-1) |
| n2 |
| 2n2-n-1 |
| 2(n+1) |
分析:(I)利用奇函数的性质f(-x)=-f(x)和对数的运算法则即可得出a;
(II)方程lnx=f(x)(x2-2ex+m),即lnx=x(x2-2ex+m)?
=(x-e)2+m-e2.令h(x)=
,g(x)=(x-e)2+m-e2.利用导数可得函数h(x)的最大值,g(x)的最小值,通过分类讨论即可得出方程的解的情况;
(III)由(Ⅱ)知当m=e2+1时,g(x)=(x-e)2+1,可得g(x)min=m-e2=1,此时g(x)min>h(x)max恒成立,于是h(x)<g(x)min=1,即
<1,化为lnx<x恒成立,则当n≥2时,有ln(n2-1)<n2-1,进而得到
<
,再利用放缩法即可证明.
(II)方程lnx=f(x)(x2-2ex+m),即lnx=x(x2-2ex+m)?
| lnx |
| x |
| lnx |
| x |
(III)由(Ⅱ)知当m=e2+1时,g(x)=(x-e)2+1,可得g(x)min=m-e2=1,此时g(x)min>h(x)max恒成立,于是h(x)<g(x)min=1,即
| lnx |
| x |
| ln(n2-1) |
| n2 |
| n2-1 |
| n2 |
解答: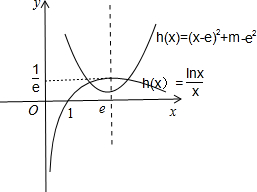 解:(Ⅰ)∵f(-x)=-f(x),
解:(Ⅰ)∵f(-x)=-f(x),
∴ln(e-x+a)=-ln(ex+a),
∴e-x+a=
,化为a(a+e-x+ex)=0,解得a=0.
(Ⅱ)方程lnx=f(x)(x2-2ex+m),即lnx=x(x2-2ex+m)?
=(x-e)2+m-e2.
令h(x)=
,g(x)=(x-e)2+m-e2.
∴h′(x)=
,
∴h(x)在(0,e)单调递增;在(e,+∞)上单调递减,
∴h(x)max=h(e)=
.
g(x)为二次函数在(0,e)上单调递减,在(e,+∞)上单调递增,
∴g(x)min=m-e2.
故①m-e2>
,即m>e2+
时,无解;
②当m-e2=
,即m=e2+
时,有一解;
③当m-e2<
,即m<e2+
时,有二解.
(Ⅲ)证明:由(Ⅱ)知当m=e2+1时,g(x)=(x-e)2+1,
∴g(x)min=m-e2=1,此时g(x)min>h(x)max恒成立,
∴h(x)<g(x)min=1,即
<1,化为lnx<x恒成立,
∴当n≥2时,有ln(n2-1)<n2-1,
∴
<
=1-
,
∴
+
+…+
<(n-1)-(
+
+…+
)
<(n-1)-(
+
+…+
)
=(n-1)-[(
-
)+(
-
)+…+(
-
)]
=(n-1)-(
-
)
=
.
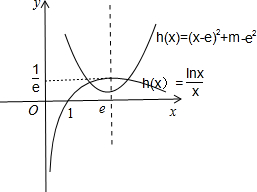 解:(Ⅰ)∵f(-x)=-f(x),
解:(Ⅰ)∵f(-x)=-f(x),∴ln(e-x+a)=-ln(ex+a),
∴e-x+a=
| 1 |
| ex+a |
(Ⅱ)方程lnx=f(x)(x2-2ex+m),即lnx=x(x2-2ex+m)?
| lnx |
| x |
令h(x)=
| lnx |
| x |
∴h′(x)=
| 1-lnx |
| x2 |
∴h(x)在(0,e)单调递增;在(e,+∞)上单调递减,
∴h(x)max=h(e)=
| 1 |
| e |
g(x)为二次函数在(0,e)上单调递减,在(e,+∞)上单调递增,
∴g(x)min=m-e2.
故①m-e2>
| 1 |
| e |
| 1 |
| e |
②当m-e2=
| 1 |
| e |
| 1 |
| e |
③当m-e2<
| 1 |
| e |
| 1 |
| e |
(Ⅲ)证明:由(Ⅱ)知当m=e2+1时,g(x)=(x-e)2+1,
∴g(x)min=m-e2=1,此时g(x)min>h(x)max恒成立,
∴h(x)<g(x)min=1,即
| lnx |
| x |
∴当n≥2时,有ln(n2-1)<n2-1,
∴
| ln(n2-1) |
| n2 |
| n2-1 |
| n2 |
| 1 |
| n2 |
∴
| ln(22-1) |
| 22 |
| ln(32-1) |
| 32 |
| ln(n2-1) |
| n2 |
<(n-1)-(
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
<(n-1)-(
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=(n-1)-[(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=(n-1)-(
| 1 |
| 2 |
| 1 |
| n+1 |
=
| 2n2-n-1 |
| 2(n+1) |
点评:本题考查不等式的证明,熟练掌握利用导数研究函数的单调性、极值与最值、分类讨论思想方法、函数的奇偶性、利用已经证明的结论解决问题、放缩法等是解题的关键,属于难题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目