题目内容
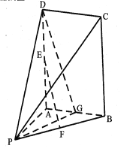
【题目】在正方体
中，点
，
分别为
，
的中点，则下列说法正确的是______.
①
平面
②
平面
③
平面
④
平面
【答案】④
【解析】
①②③错误，采用反证，假设正确，再根据线面垂直，线面平行的性质推出矛盾；④先证明
，再对称考虑有
，最后通过线面垂直的判定推出结论.
①连接
，
，有
，
，故
平面
.假设
平面,则有
，而
，故平面
，于是
，矛盾，所以此命题错误.
②设与交于
，则
，
，故四边形
是平行四边形，所以有
.假设
平面
，因在平面上，故
也在平面上，而直线
直线和为异面直线，矛盾，所以此命题错误.
③假设
平面
，则必有
，而又有
，故
平面
.于是有
，矛盾，所以此命题错误.
④连接
，则有
，又因为
，所以有
，故
.
是
的中点，由正方形性质，，
，三点共线.所以平面
即是平面
，同理设
的中点为
，则
，于是有
平面，故平面.
故本题的答案为：④
练习册系列答案
阅读快车系列答案
相关题目
