题目内容
已知 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足 .令
.令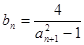
 ,记数列
,记数列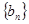 的前
的前 项和为
项和为 ,对任意的
,对任意的 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的最小值是 .
的最小值是 .
100
解析试题分析:根据题意,由于 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足
 ,则可知
,则可知 ,故可知数列
,故可知数列 的通项公式为5+2(n-3)=2n-1,因为
的通项公式为5+2(n-3)=2n-1,因为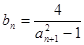 =
= ,因此可知数列
,因此可知数列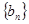 的前
的前 项和为
项和为 =1-
=1- =
=  ,因为不等式
,因为不等式 恒成立,则可知m的最小值为100.故答案为100.
恒成立,则可知m的最小值为100.故答案为100.
考点:等差数列
点评:主要是考查了等差数列的通项公式以及求和的运用,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
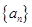 满足
满足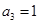 ,
,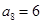 ,则此数列的前
,则此数列的前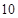 项的和
项的和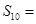 .
.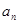 }的前
}的前 项和
项和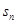 满足
满足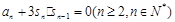 ,
,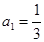 ,则
,则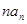 的最小值为 .
的最小值为 . 的前三项依次为
的前三项依次为 ,
, ,
, ,则
,则 .
.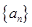 中,
中, ;设数列
;设数列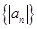 的前
的前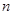 项和为
项和为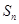 ,则
,则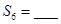
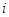 行第
行第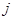 列的数记为
列的数记为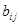 (
(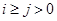 ),则
),则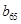 = .
= .
 满足
满足 ,
, ,则它的前10项的和
,则它的前10项的和 _____
_____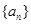 前10项的和等于前5项的和,若
前10项的和等于前5项的和,若 ,则
,则 ________。
________。