题目内容
已知数列{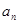 }的前
}的前 项和
项和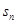 满足
满足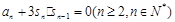 ,
,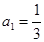 ,则
,则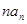 的最小值为 .
的最小值为 .
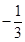
解析试题分析:因为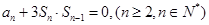 ,所以
,所以 因为
因为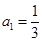 ,显然
,显然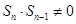 化简得
化简得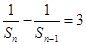 ,可见
,可见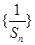 是以
是以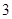 为首项,
为首项,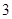 为公差的等差数列,所以
为公差的等差数列,所以 ,从而
,从而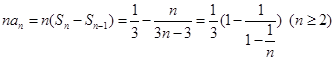 ,要使
,要使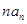 最小则需
最小则需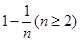 最小,即
最小,即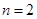 时最小,此时
时最小,此时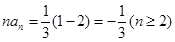 ,当
,当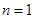 时,
时,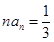 ,故对任意的
,故对任意的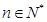 ,
,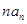 最小为
最小为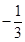 .
.
考点:1.数列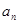 和前
和前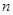 项和
项和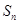 的关系;2.等差数列.
的关系;2.等差数列.

练习册系列答案
相关题目
题目内容
已知数列{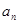 }的前
}的前 项和
项和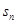 满足
满足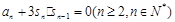 ,
,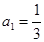 ,则
,则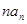 的最小值为 .
的最小值为 .
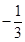
解析试题分析:因为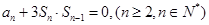 ,所以
,所以 因为
因为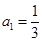 ,显然
,显然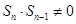 化简得
化简得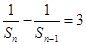 ,可见
,可见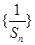 是以
是以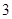 为首项,
为首项,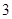 为公差的等差数列,所以
为公差的等差数列,所以 ,从而
,从而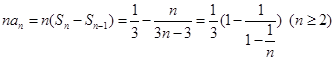 ,要使
,要使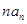 最小则需
最小则需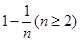 最小,即
最小,即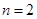 时最小,此时
时最小,此时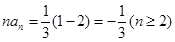 ,当
,当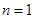 时,
时,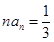 ,故对任意的
,故对任意的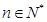 ,
,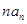 最小为
最小为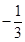 .
.
考点:1.数列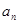 和前
和前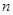 项和
项和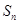 的关系;2.等差数列.
的关系;2.等差数列.
