题目内容
若△ABC的内角满足sinA+cosA>0,tanA-sinA<0,则角A的取值范围是( )
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
分析:分别解两个不等式,再求它们的交集即可.
解答:解:sinA+cosA=
sin(A+
)>0,又0<A<π,故0<A<
π,
tanA-sinA<0,即
-sinA< 0,又sinA>0,cosA<1,故cosA<0,即
π<A<π 综上,
π<A<
π,
故选C.
| 2 |
| π |
| 4 |
| 3 |
| 4 |
tanA-sinA<0,即
| sinA |
| cosA |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
故选C.
点评:本题主要考查三角函数的化简,及与三角形的综合,应注意三角形内角的范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
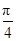 ) B.(
) B.(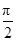 ) C.(
) C.(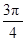 ) D.(
) D.(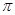 )
)