题目内容
(08年龙岩一中冲刺理)(12分)
已知双曲线![]() 的两个焦点为
的两个焦点为![]() ,
,![]() ,
,![]() 为动点,若
为动点,若![]() ,
,![]() 为定值(其中
为定值(其中![]() >1),
>1),![]() 的最小值为
的最小值为![]() .
.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设点![]() ,过点
,过点![]() 作直线
作直线![]() 交轨迹
交轨迹![]() 于
于![]() ,
,![]() 两点,判断
两点,判断![]() 的大小是否为定值?并证明你的结论.
的大小是否为定值?并证明你的结论.
解析:(Ⅰ)依题意点![]() 的轨迹为以双曲线
的轨迹为以双曲线![]() 的两个焦点为焦点,且长轴为
的两个焦点为焦点,且长轴为![]() 的椭圆。设椭圆方程为
的椭圆。设椭圆方程为![]() (
(![]() ) ………………1分
) ………………1分
由双曲线![]() 方程,得双曲线两个焦点为
方程,得双曲线两个焦点为![]() (-1,0),
(-1,0),![]() (1,0),设
(1,0),设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由余弦定理得![]() ………3分
………3分
又 ![]() ,当
,当![]() 时取“=”,即
时取“=”,即![]()
∴ ![]() ,得
,得![]() ∴
∴ ![]()
∴ 动点![]() 轨迹
轨迹![]() 方程为
方程为![]() ………………6分
………………6分
(Ⅱ)当![]() 轴时,直线
轴时,直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 解得
解得![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 而
而![]() ,∴
,∴![]() ,
,
猜测![]() 为定值。 ………………………7分
为定值。 ………………………7分
证明:设直线![]() 的方程为
的方程为![]() ,
,
由 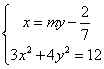 ,得
,得![]()
∴![]() ,
,![]() ………………9分
………………9分
∴![]()
![]()
![]()
![]()
![]()
∴ ![]() 为定值. ………………………12分
为定值. ………………………12分

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
