题目内容
函数 ,关于方程
,关于方程 有三个不同实数解,则实数
有三个不同实数解,则实数 的取值范围为( )
的取值范围为( )
A. | B. |
C. | D. |
D
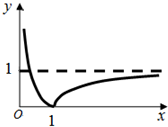
解析试题分析:函数 ,根据
,根据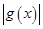 的图象,设
的图象,设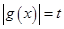 ,∵关于
,∵关于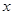 x的方程
x的方程 有有三个不同的实数解,即为
有有三个不同的实数解,即为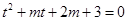 有两个根,且一个在
有两个根,且一个在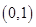 上,一个在
上,一个在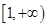 上.设
上.设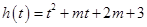 ,①当有一个根为
,①当有一个根为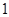 时,
时,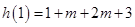 ,
,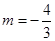 ,此时另一根为
,此时另一根为 ,符合题意.②当没有根为
,符合题意.②当没有根为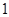 时,则:
时,则: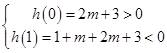 ,解得
,解得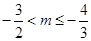 ,综上可得,m的取值范围是
,综上可得,m的取值范围是 .
.
考点:对数函数图象与性质的综合应用.

练习册系列答案
相关题目
在对数函数 中,下列描述正确的是( )
中,下列描述正确的是( )
①定义域是 、值域是R ②图像必过点(1,0).
、值域是R ②图像必过点(1,0).
③当 时,在
时,在 上是减函数;当
上是减函数;当 时,在
时,在 上是增函数.
上是增函数.
④对数函数既不是奇函数,也不是偶函数.
| A.①② | B.②③ | C.①②④ | D.①②③④ |
函数 的定义域是
的定义域是
| A.[1,2] | B. | C. | D. |
若 ,则
,则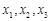 的大小关系为( )
的大小关系为( )
A. < < < < | B. < < < < | C. < < < < | D. < < < < |
若 ,则
,则 ()
()
A.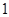 | B. | C. | D.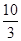 |
设 ,
, ,
, ,则( )
,则( )
A. | B. | C.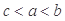 | D. |
函数f(x)=x2+lnx 4的零点所在的区间是( )
4的零点所在的区间是( )
| A.(0,1) | B.(1,2) | C.(2,3) | D.(3,4) |
定义在 上的奇函数
上的奇函数 满足:当
满足:当 时,
时, ,则方程
,则方程 的实数根的个数是( )
的实数根的个数是( )
| A.1 | B.2 | C.3 | D.5 |
 小时
小时 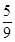 小时
小时