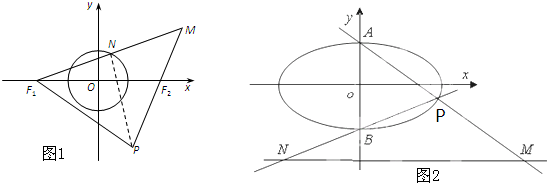
题目内容
点P在椭圆
+
=1上运动,Q、R分别在两圆(x+1)2+y2=1和(x-1)2+y2=1上运动,则|PQ|+|PR|的最大值为( )
| x2 |
| 4 |
| y2 |
| 3 |
分析:椭圆
+
=1中,c2=4-3=1,故椭圆
+
=1两焦点F1(-1,0),F2(1,0)恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心,过P点作x轴平行线,分别交两准线于A,B两点,连接PF1,PF2,并延长,分别交两圆于Q′,R′,则|PQ|+|PR|≤|PQ′|+|PR′|=|PF1|+1+|PF2|+1=e|AB|+2,由此能求出|PQ|+|PR|的最大值.
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
解答:解:∵椭圆
+
=1中,c2=4-3=1,
∴椭圆
+
=1两焦点F1(-1,0),F2(1,0)恰为两圆(x+1)2+y2=1和(x-1)2+y2=1的圆心,
e=
=
,准线x=±
=±4,
过P点作x轴平行线,分别交两准线于A,B两点,
连接PF1,PF2,并延长,分别交两圆于Q′,R′,
则|PQ|+|PR|≤|PQ′|+|PR′|
=|PF1|+1+|PF2|+1
=e|PA|+e|PB|+2
=e|AB|+2
=
×8+2
=6.
故选D.
| x2 |
| 4 |
| y2 |
| 3 |
∴椭圆
| x2 |
| 4 |
| y2 |
| 3 |
e=
| c |
| a |
| 1 |
| 2 |
| a2 |
| c |

过P点作x轴平行线,分别交两准线于A,B两点,
连接PF1,PF2,并延长,分别交两圆于Q′,R′,
则|PQ|+|PR|≤|PQ′|+|PR′|
=|PF1|+1+|PF2|+1
=e|PA|+e|PB|+2
=e|AB|+2
=
| 1 |
| 2 |
=6.
故选D.
点评:本题考查椭圆和圆的简单性质,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
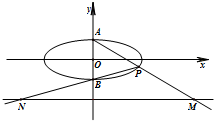 在平面直角坐标系xOy中,如图,已知椭圆C:
在平面直角坐标系xOy中,如图,已知椭圆C: