题目内容
(1)如图1,已知定点F1(-2,0)、F2(2,0),动点N满足|
|=1(O为坐标原点),
=2
,
=λ
(λ∈R),
•
=0,求点P的轨迹方程.
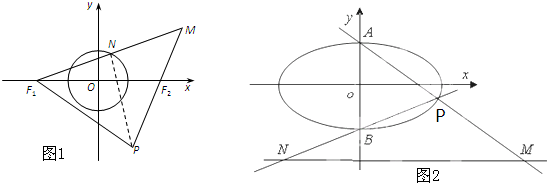
(2)如图2,已知椭圆C:
+y2=1的上、下顶点分别为A、B,点P在椭圆上,且异于点A、B,直线AP、BP与直线l:y=-2分别交于点M、N,
(ⅰ)设直线AP、BP的斜率分别为k1、k2,求证:k1•k2为定值;
(ⅱ)当点P运动时,以MN为直径的圆是否经过定点?请证明你的结论.
| ON |
| F1M |
| NM |
| MP |
| MF2 |
| F1M |
| PN |

(2)如图2,已知椭圆C:
| x2 |
| 4 |
(ⅰ)设直线AP、BP的斜率分别为k1、k2,求证:k1•k2为定值;
(ⅱ)当点P运动时,以MN为直径的圆是否经过定点?请证明你的结论.
分析:(1)由双曲线的定义可知:点P的轨迹是以F1,F2为焦点的双曲线,从而可得点P的轨迹方程;
(2)(ⅰ)由椭圆方程求出两个顶点A,B的坐标,设出P点坐标,写出直线AP、BP的斜率k1,k2,结合P的坐标适合椭圆方程可证结论;
(ⅱ)设出以MN为直径的圆上的动点Q的坐标,由
•
=0列式得到圆的方程,化为圆系方程后联立方程组可求解圆所过定点的坐标.
(2)(ⅰ)由椭圆方程求出两个顶点A,B的坐标,设出P点坐标,写出直线AP、BP的斜率k1,k2,结合P的坐标适合椭圆方程可证结论;
(ⅱ)设出以MN为直径的圆上的动点Q的坐标,由
| QM |
| QN |
解答:解:(1)连接ON,
∵
=2
,∴点N是MF1中点,∴|MF2|=2|NO|=2
∵
•
=0,∴F1M⊥PN,∴|PM|=|PF1|
∴||PF1|-|PF2||=||PM|-|PF2||=|MF2|=2<|F1F2|
由双曲线的定义可知:点P的轨迹是以F1,F2为焦点的双曲线.
∴点P的轨迹方程是x2-
=1;
(2)(ⅰ)令P(x0,y0),则由题设可知x0≠0,
∵A(0,1),B(0,-1),
∴直线AP的斜率k1=
,PB的斜率k2=
,
又点P在椭圆上,∴
+y02=1,
从而有k1k2=
•
=
=-
;
(ⅱ)设Q(x,y)是以MN为直径的圆上的任意一点,则
•
=0,
∴有(x+
)•(x+
)+(y+2)(y+2)=0
又k1•k2=-
,
∴MN为直径圆的方程为x2+(y+2)2-12+(
-4k1)x=0.
令
,解得
,
∴以MN为直径的圆恒过定点(0,-2+
)或(0,-2-2
).
∵
| F1M |
| NM |
∵
| F1M |
| PN |
∴||PF1|-|PF2||=||PM|-|PF2||=|MF2|=2<|F1F2|
由双曲线的定义可知:点P的轨迹是以F1,F2为焦点的双曲线.
∴点P的轨迹方程是x2-
| y2 |
| 3 |
(2)(ⅰ)令P(x0,y0),则由题设可知x0≠0,
∵A(0,1),B(0,-1),
∴直线AP的斜率k1=
| y0-1 |
| x0 |
| y0+1 |
| x0 |
又点P在椭圆上,∴
| x02 |
| 4 |
从而有k1k2=
| y0-1 |
| x0 |
| y0+1 |
| x0 |
| y02-1 |
| x02 |
| 1 |
| 4 |
(ⅱ)设Q(x,y)是以MN为直径的圆上的任意一点,则
| QM |
| QN |
∴有(x+
| 1 |
| k1 |
| 1 |
| k2 |
又k1•k2=-
| 1 |
| 4 |
∴MN为直径圆的方程为x2+(y+2)2-12+(
| 3 |
| k1 |
令
|
|
∴以MN为直径的圆恒过定点(0,-2+
| 3 |
| 3 |
点评:本题考查了直线的斜率,考查了直线与圆锥曲线的关系,考查代入法,考查了圆系方程,考查了学生的计算能力,是有一定难度题目.

练习册系列答案
相关题目
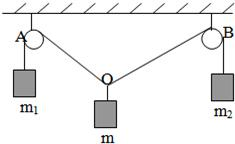 如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证:
如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证: 如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.
如图,已知二面角α-l-β的平面角为45°,在半平面α内有一个半圆O,其直径AB在l上,M是这个半圆O上任一点(除A、B外),直线AM、BM与另一个半平面β所成的角分别为θ1、θ2.试证明cos2θ1+cos2θ2为定值.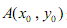 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P
、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P
、Q. 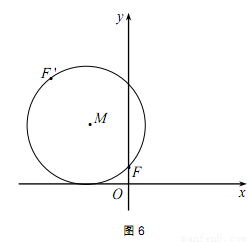
 :
: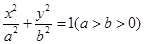 的离心率为
的离心率为 ,以椭圆
,以椭圆 为
为 ,设圆
,设圆 与点
与点 .
. 的最小值,并求此时圆
的最小值,并求此时圆 是椭圆
是椭圆 的任意一点,且直线
的任意一点,且直线 分别与
分别与 轴交于点
轴交于点 ,
, 为坐标原点,求证:
为坐标原点,求证: 为定值.
为定值.