题目内容
设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为 =0.85x-85.71,则下列结论中不正确的是( ).
=0.85x-85.71,则下列结论中不正确的是( ).
| A.y与x具有正的线性相关关系 |
B.回归直线过样本点的中心( , , ) ) |
| C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg |
| D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg |
D
解析试题分析:因为,x的系数为正数,所以,A.y与x具有正的线性相关关系,正确;
由回归直线的性质,B.回归直线过样本点的中心( ,
, ),C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg,正确;只有D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg,不正确,故选D。
),C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg,正确;只有D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg,不正确,故选D。
考点:变量的相关性,回归直线的性质,回归直线方程的应用。
点评:简单题,综合考查变量的相关性,回归直线的性质,回归直线方程的应用,难度不大,突出对基础知识的考查。

为了解一片速生林的生长情况,随机测量了其中100株树木的 底部周长(单位:cm).根据所得数据画出了样本的频率分布直方图,那么在这100株树木中,底部周长小于110cm的株数是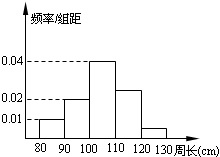
| A.80 | B.70 | C.60 | D.30 |
某大学中文系共有本科生5000人,其中一、二、三、四年级的学生比为5:4:3:1,要用分层抽样的方法从该系所有本科生中抽取一个容量为260的样本,则应抽二年级的学生( )
| A.100人 | B.80人 | C.60人 | D.20人 |
为了评价某个电视栏目的改革效果,在改革前后分别从某居民点抽取了1000位居民进行调查,经过计算得K2 4.358,根据这一数据分析,下列说法正确的是( )
4.358,根据这一数据分析,下列说法正确的是( )
| A.有95%的人认为该栏日优秀 |
| B.有95%的人认为该栏目是否优秀与改革有关系 |
| C.有95%的把握认为电视栏目是否优秀与改革有关系 |
| D.没有理由认为电视栏目是否优秀与改革有关系 |
某交警部门对城区上下班交通情况作抽样调查,上下班时间各抽取12辆机动车的行驶速度(单位:km/h)作为样本进行研究,做出样本的茎叶图,则上班、下班时间行驶速度的中位数分别是( )
| A.2827.5 | B.2828.5 |
| C.2927.5 | D.2928.5 |
某班有50名同学,将其编为1、2、3、…、50号,并按编号从小到大平均分成5组.现用系统抽样方法,从该班抽取5名同学进行某项调查,若第1组抽取的学生编号为3,第2组抽取的学生编号为13,则第4组抽取的学生编号为
| A.14 | B.23 | C.33 | D.43 |
从2003件产品中选取50件,若采用下面的方法选取:先用简单随机抽样从2003件产品中剔除3件,剩下的2000件再按系统抽样的方法抽取,则每件产品被选中的概率
| A.不都相等 | B.都不相等 | C.都相等,且为 | D.都相等,且为 |


 的值为( )
的值为( )

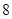


 个得分去掉
个得分去掉 个最高分,去掉
个最高分,去掉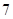 个剩余分数的平均分为
个剩余分数的平均分为 ,现场做的
,现场做的 表示:
表示: