题目内容
当0<x<时,函数f(x)=的最小值是 ( )
A.4 B. C.2 D.
A
解析试题分析:∵f(x)=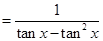 ,令t=
,令t=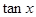 ,由0<x<得
,由0<x<得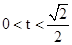 ,∴
,∴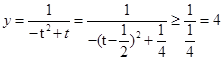 ,故选A
,故选A
考点:本题考查了复合函数的最值求法
点评:对于可化为一元二次函数类型的函数最值求解,要注意换元后参数的范围

练习册系列答案
相关题目
设 ,则( )
,则( )
A. | B. | C. | D. |
已知函数 的两个零点分别在区间
的两个零点分别在区间 和区间
和区间 内,则实数
内,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
如果函数
 =x
=x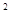 +2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )。
+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )。
| A.a≥-3 | B. a≤-3 | C. a≤5 | D. a≥3 |
幂函数 的图象过点
的图象过点 且
且 ,则实数
,则实数 的所有可能的值为
的所有可能的值为
A.4或 | B. | C.4或 | D. 或2 或2 |
已知函数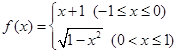 , 则
, 则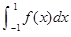 的值为
的值为
A. | B.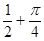 | C.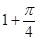 | D.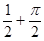 |
已知 ,且函数
,且函数 恰有3个不同的零点,则实数a的取值范围是
恰有3个不同的零点,则实数a的取值范围是
A.(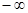 ,l] ,l] | B.(O,1] | C.(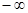 ,O] ,O] | D.(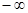 ,2] ,2] |
若 ,不等式
,不等式 的解集为
的解集为 ,关于
,关于 的不等式
的不等式 的解集记为
的解集记为 ,已知
,已知 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知 则
则 的解集为( )
的解集为( )
A.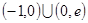 | B. |
C. | D.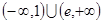 |