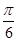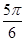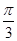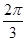题目内容
已知向量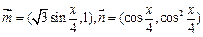 .(1)若
.(1)若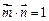 ,求
,求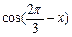 的值;(2)记
的值;(2)记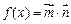 ,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
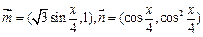 .(1)若
.(1)若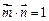 ,求
,求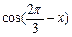 的值;(2)记
的值;(2)记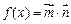 ,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.(Ⅰ)  (Ⅱ)
(Ⅱ) 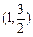
 (Ⅱ)
(Ⅱ) 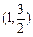
(1)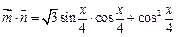
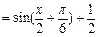
∵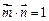 ∴
∴ ┉┉4分
┉┉4分
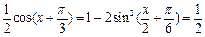
 ┉┉7分
┉┉7分
(2)∵(2a-c)cosB=bcosC 由正弦定理得(2sinA-sinC)cosB=sinBcosC┉8分
∴2sinAcosB-sinCcosB="sinBcosC " ∴2sinAcosB=sin(B+C)
∵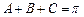 ∴
∴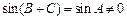 ,
,
∴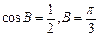 ┉┉┉┉┉┉10分∴
┉┉┉┉┉┉10分∴ ┉11分
┉11分
∴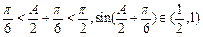 ┉┉┉┉┉┉12分
┉┉┉┉┉┉12分
又∵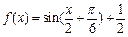 ,∴
,∴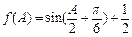 ┉┉┉┉┉┉13分
┉┉┉┉┉┉13分
故函数f(A)的取值范围是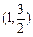 ┉┉┉┉┉┉14分
┉┉┉┉┉┉14分
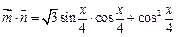
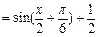
∵
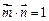 ∴
∴ ┉┉4分
┉┉4分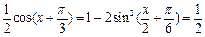
 ┉┉7分
┉┉7分(2)∵(2a-c)cosB=bcosC 由正弦定理得(2sinA-sinC)cosB=sinBcosC┉8分
∴2sinAcosB-sinCcosB="sinBcosC " ∴2sinAcosB=sin(B+C)
∵
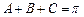 ∴
∴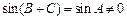 ,
,∴
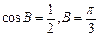 ┉┉┉┉┉┉10分∴
┉┉┉┉┉┉10分∴ ┉11分
┉11分∴
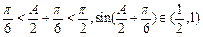 ┉┉┉┉┉┉12分
┉┉┉┉┉┉12分又∵
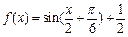 ,∴
,∴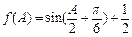 ┉┉┉┉┉┉13分
┉┉┉┉┉┉13分故函数f(A)的取值范围是
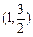 ┉┉┉┉┉┉14分
┉┉┉┉┉┉14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
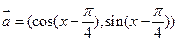 ,
,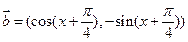 ,
, 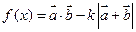 ,
, 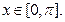
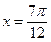 ,求
,求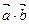 及
及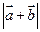 ;
;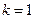 ,当
,当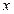 为何值时,
为何值时,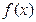 有最小值,最小值是多少?
有最小值,最小值是多少?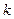 的值.
的值.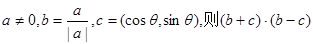 =
= 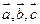 所成的角均相等,且
所成的角均相等,且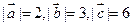 ,求
,求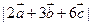 的值。
的值。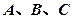 是直线
是直线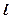 上不同的三个点,点
上不同的三个点,点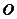 不在
不在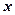 的方程
的方程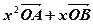 +
+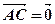 的解集为 ( )
的解集为 ( )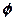
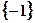

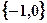
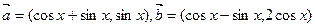 ,设
,设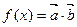 .
.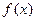 的最小正周期,并写出
的最小正周期,并写出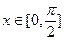 时,求函数
时,求函数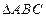 内部,且有
内部,且有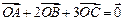 ,则
,则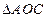 的面积的比为( )
的面积的比为( )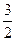
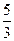
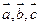 三向量两两所成的角相等,并且
三向量两两所成的角相等,并且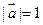 ,
,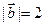 ,
,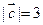 ,试求向量
,试求向量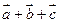 的长度以及与已知三向量的夹角.
的长度以及与已知三向量的夹角.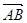 ,
,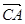 〉的大小为()
〉的大小为()