题目内容
 如图,已知ABC-A1B1C1是正三棱柱,D是AC的中点,∠C1DC=60°.
如图,已知ABC-A1B1C1是正三棱柱,D是AC的中点,∠C1DC=60°.(Ⅰ)求证:AB1∥平面BC1D;
(Ⅱ)求二面角D-BC1-C的大小.
分析:(Ⅰ)以AC的中点D为原点建立如图所示的空间直角坐标系,设AD=1,证明
=2
,利用线面平行的判定定理,即可得到结论;
(II)确定平面BC1D的一个法向量、平面BCC1B1的一个法向量,利用向量的夹角公式,可求二面角D-BC1-C的大小.
| AB1 |
| DO |
(II)确定平面BC1D的一个法向量、平面BCC1B1的一个法向量,利用向量的夹角公式,可求二面角D-BC1-C的大小.
解答: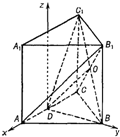 解:(Ⅰ)以AC的中点D为原点建立如图所示的空间直角坐标系,设AD=1.
解:(Ⅰ)以AC的中点D为原点建立如图所示的空间直角坐标系,设AD=1.
∵∠C1DC=60°,∴CC1=
则A(1,0,0),B(0,
,0),C(-1,0,0),A1(1,0,
),
B1(0,
,
),C1(-1,0,
)
连结B1C交BC1于O,则O是B1C的中点,连结DO,则O(-
,
,
)
∴
=(-1,
,
),
=(-
,
,
),
∴
=2
.
∵AB1?平面BC1D,DO?平面BC1D,
∴AB1∥平面BC1D.…(5分)
(Ⅱ)
=(-1,0,
),
=(1,
,-
).
设平面BC1D的一个法向量为
=(x,y,z),则
即
,则有y=0
令z=1,则
=(
,0,1),设平面BCC1B1的一个法向量是为
=(x',y',z'),
=(0,0,
),
=(1,
,-
),则
即
,∴z′=0.
令y'=-1,则
=(
,-1,0)
∴cos<
,
>=
=
∴二面角D-BC1-C的大小为arccos
.…(12分)
 解:(Ⅰ)以AC的中点D为原点建立如图所示的空间直角坐标系,设AD=1.
解:(Ⅰ)以AC的中点D为原点建立如图所示的空间直角坐标系,设AD=1.∵∠C1DC=60°,∴CC1=
| 3 |
则A(1,0,0),B(0,
| 3 |
| 3 |
B1(0,
| 3 |
| 3 |
| 3 |
连结B1C交BC1于O,则O是B1C的中点,连结DO,则O(-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| AB1 |
| 3 |
| 3 |
| DO |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴
| AB1 |
| DO |
∵AB1?平面BC1D,DO?平面BC1D,
∴AB1∥平面BC1D.…(5分)
(Ⅱ)
| DC1 |
| 3 |
| C1B |
| 3 |
| 3 |
设平面BC1D的一个法向量为
| n |
|
即
|
令z=1,则
| n |
| 3 |
| m |
| CC1 |
| 3 |
| C1B |
| 3 |
| 3 |
|
即
|
令y'=-1,则
| m |
| 3 |
∴cos<
| m |
| n |
| ||||
|
|
| 3 |
| 4 |
∴二面角D-BC1-C的大小为arccos
| 3 |
| 4 |
点评:本题考查线面平行,考查二面角的平面角,考查向量知识的运用,确定平面的法向量 是关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
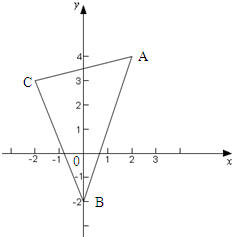 如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求: 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证: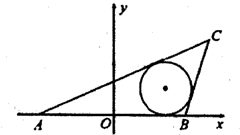 如图,已知两点A(-
如图,已知两点A(-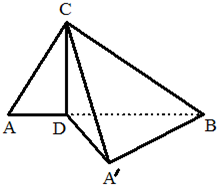
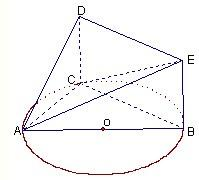 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,