题目内容
设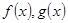 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当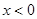 时,
时, ,且
,且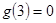 ,则不等式
,则不等式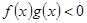 的解集为
的解集为
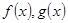 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当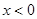 时,
时, ,且
,且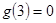 ,则不等式
,则不等式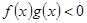 的解集为
的解集为A. | B. |
C. | D. |
D
因为当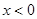 时,
时, ,所以
,所以 在
在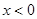 时为增函数。又
时为增函数。又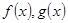 分别是定义在R上的奇函数和偶函数,所以
分别是定义在R上的奇函数和偶函数,所以 为奇函数,从而
为奇函数,从而 时
时 为增函数且
为增函数且 ,故不等式
,故不等式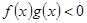 的解集为
的解集为 。
。
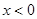 时,
时, ,所以
,所以 在
在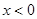 时为增函数。又
时为增函数。又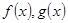 分别是定义在R上的奇函数和偶函数,所以
分别是定义在R上的奇函数和偶函数,所以 为奇函数,从而
为奇函数,从而 时
时 为增函数且
为增函数且 ,故不等式
,故不等式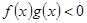 的解集为
的解集为 。
。
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
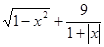 是( ).
是( ). 是奇函数,且
是奇函数,且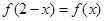 ,当
,当 时,
时, ,当
,当 时,
时, ( )
( )



 是偶函数,当
是偶函数,当 时,
时, ,且当
,且当 时,
时, 恒成立,则
恒成立,则 的最小值是( )
的最小值是( )


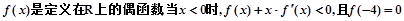 ,则不等式
,则不等式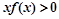 的解集为( )
的解集为( )



 上是增函数的是
上是增函数的是



 是定义在R上的奇函数,当x≥0时,
是定义在R上的奇函数,当x≥0时, ,则函数在x<0时的解析式是
,则函数在x<0时的解析式是 = 。
= 。 ,若
,若 ,则
,则 。
。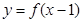 为奇函数,
为奇函数,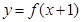 为偶函数(定义域均为R)若
为偶函数(定义域均为R)若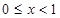 时:
时: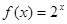 ,则
,则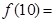 _________.
_________.