题目内容
已知直线上n个点最多将直线分成
+
=n+1段,平面上n条直线最多将平面分成
+
+
=
部分(规定:若k>n则
=0),则类似地可以推算得到空间里n个平面最多将空间分成
+
+
+
+
+
+
部分.
| C | 0 n |
| C | 1 n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| n2+n+2 |
| 2 |
| C | k n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
分析:根据直线类比到平面,再类比到空间,分析所给规律,即可得到结论.
解答:解:根据直线上n个点最多将直线分成
+
=n+1段,平面上n条直线最多将平面分成
+
+
=
部分,我们类比可得空间里n个平面最多将空间分成
+
+
+
部分
故答案为:
+
+
+
| C | 0 n |
| C | 1 n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| n2+n+2 |
| 2 |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
故答案为:
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
点评:本题考查归纳推理的应用,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 段,平面上n条直线最多将平面分成
段,平面上n条直线最多将平面分成 部分(规定:若k>n则
部分(规定:若k>n则 =0),则类似地可以推算得到空间里n个平面最多将空间分成________部分.
=0),则类似地可以推算得到空间里n个平面最多将空间分成________部分. 段,平面上n条直线最多将平面分成
段,平面上n条直线最多将平面分成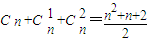 部分(规定:若k>n则
部分(规定:若k>n则 =0),则类似地可以推算得到空间里n个平面最多将空间分成 部分.
=0),则类似地可以推算得到空间里n个平面最多将空间分成 部分.