题目内容
已知集合A={x|1＜ax＜2}，B={x||x|＜1}，满足A⊆B，则实数a的范围为______．
∵B={x||x|＜1}，
∴B={x|-1＜x＜1}，
∵A⊆B，
∴①A=∅时，a=0，
②a＞0时，A={x|
＜x＜
}，
∴
≤1，解得a≥2；
③a＜0时，A={x|
＜x＜
}，
∴
≥-1，解得a≤-2；
综上数a的范围为a=0，或a≥2，或a≤-2．
故答案为{a|a=0，或a≥2，或a≤-2}．
∴B={x|-1＜x＜1}，
∵A⊆B，
∴①A=∅时，a=0，
②a＞0时，A={x|
| 1 |
| a |
| 2 |
| a |
∴
| 2 |
| a |
③a＜0时，A={x|
| 2 |
| a |
| 1 |
| a |
∴
| 2 |
| a |
综上数a的范围为a=0，或a≥2，或a≤-2．
故答案为{a|a=0，或a≥2，或a≤-2}．
练习册系列答案
相关题目
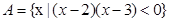，函数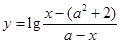
的定义域为集合B.
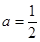时，求集合
;
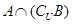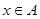,命题q: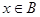 
,若q是p的必要条件，求实数a的取值范围.