题目内容
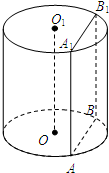
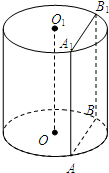 已知圆柱OO1的底面半径为13cm,高为10cm,一平面平行于圆柱OO1的轴OO1,且与轴OO1的距离为5cm,截圆柱得矩形ABB1A1.(1)求圆柱的侧面积与体积;(2)求截面ABB1A1的面积.
已知圆柱OO1的底面半径为13cm,高为10cm,一平面平行于圆柱OO1的轴OO1,且与轴OO1的距离为5cm,截圆柱得矩形ABB1A1.(1)求圆柱的侧面积与体积;(2)求截面ABB1A1的面积.
解:(1)圆柱OO1的底面半径为13cm,高为10cm,
一平面平行于圆柱OO1的轴OO1,且与轴OO1的距离为5cm,截圆柱得矩形ABB1A1的边长为24cm,
所以圆柱的侧面积为2πRh=2×10×13π=260π(cm2).
体积为πR2h=132×10π=1690π(cm3).
(2)截圆柱得矩形ABB1A1的上底边边长为:24,
所以截面面积为:10×24=240cm2.
分析:(1)通过题意求出圆柱的底面周长,然后利用侧面积公式与体积公式,直接求出侧面积,与体积.
(2)利用勾股定理,求出截面上底面的边长AB,即可求出截面面积.
点评:本题是基础题,考查旋转体与截面面积、体积的关系,考查空间想象能力,计算能力.
一平面平行于圆柱OO1的轴OO1,且与轴OO1的距离为5cm,截圆柱得矩形ABB1A1的边长为24cm,
所以圆柱的侧面积为2πRh=2×10×13π=260π(cm2).
体积为πR2h=132×10π=1690π(cm3).
(2)截圆柱得矩形ABB1A1的上底边边长为:24,
所以截面面积为:10×24=240cm2.
分析:(1)通过题意求出圆柱的底面周长,然后利用侧面积公式与体积公式,直接求出侧面积,与体积.
(2)利用勾股定理,求出截面上底面的边长AB,即可求出截面面积.
点评:本题是基础题,考查旋转体与截面面积、体积的关系,考查空间想象能力,计算能力.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
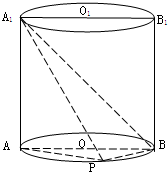 如图已知点P在圆柱OO1的底面圆周上,AB为圆O的直径,
如图已知点P在圆柱OO1的底面圆周上,AB为圆O的直径,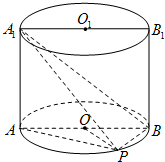 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°. 已知圆柱OO1的底面半径为13cm,高为10cm,一平面平行于圆柱OO1的轴OO1,且与轴OO1的距离为5cm,截圆柱得矩形ABB1A1.(1)求圆柱的侧面积与体积;(2)求截面ABB1A1的面积.
已知圆柱OO1的底面半径为13cm,高为10cm,一平面平行于圆柱OO1的轴OO1,且与轴OO1的距离为5cm,截圆柱得矩形ABB1A1.(1)求圆柱的侧面积与体积;(2)求截面ABB1A1的面积.