题目内容
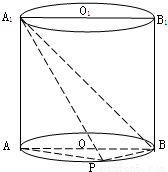
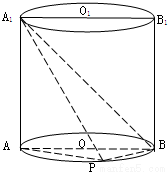
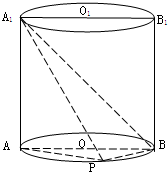 如图已知点P在圆柱OO1的底面圆周上,AB为圆O的直径,
如图已知点P在圆柱OO1的底面圆周上,AB为圆O的直径,(1)求证:BP⊥A1P;
(2)若圆柱的体积为12π,OA=2,∠AOP=120°,求异面直线A1B与AP所成角大小.
分析:(1)根据圆柱的几何特征及圆周角定理,我们易根据已知中点P在圆柱OO1的底面圆周上,AB为圆O的直径,得到AP⊥BP,AA1⊥BP,结合线面垂直的判定定理得到BP⊥平面PAA1后,易进一步得到BP⊥A1P;
(2)延长PO交圆O于点Q,连接BQ,A1Q,结合圆柱的体积为12π,OA=2,∠AOP=120°,我们易得∠A1BQ即为异面直线A1B与AP所成角,利用余弦定理求出其余弦值,即可得到答案.
(2)延长PO交圆O于点Q,连接BQ,A1Q,结合圆柱的体积为12π,OA=2,∠AOP=120°,我们易得∠A1BQ即为异面直线A1B与AP所成角,利用余弦定理求出其余弦值,即可得到答案.
解答:解:(1)证明:易知AP⊥BP,又由AA1⊥平面PAB,得AA1⊥BP,(2分)
从而BP⊥平面PAA1,故BP⊥A1P;(5分)
(2)解:延长PO交圆O于点Q,连接BQ,A1Q,则BQ∥AP,得∠A1BQ或它的补角为异面直线A1B与AP所成的角.(7分)
由题意V=π•OA2•AA1=4π•AA1=12π,解得AA1=3.(8分)
又BQ=2
,AQ=2,得A1Q=
,A1B=5,(11分)
由余弦定理得cos∠A1BQ=
=
>0,(13分)
得异面直线A1B与AP所成的角为arc cos
.(14分)
从而BP⊥平面PAA1,故BP⊥A1P;(5分)
(2)解:延长PO交圆O于点Q,连接BQ,A1Q,则BQ∥AP,得∠A1BQ或它的补角为异面直线A1B与AP所成的角.(7分)
由题意V=π•OA2•AA1=4π•AA1=12π,解得AA1=3.(8分)
又BQ=2
| 3 |
| 13 |
由余弦定理得cos∠A1BQ=
| A1B2+BQ2-A1Q2 |
| 2A1B•BQ |
2
| ||
| 5 |
得异面直线A1B与AP所成的角为arc cos
2
| ||
| 5 |
点评:本题考查的知识点是直线与平面垂直的性质及异面直线及其所成的角,其中熟练掌握圆柱的几何特征,并从中分析出相关直线之间的位置关系是解答本题的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
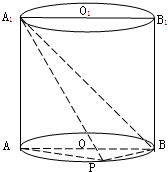 如图已知点P在圆柱OO1的底面圆周上,AB为圆O的直径,
如图已知点P在圆柱OO1的底面圆周上,AB为圆O的直径,