题目内容
(本小题满分12分)
设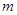 是实数,
是实数,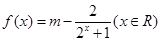 ,
,
(1)若函数 为奇函数,求
为奇函数,求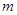 的值;
的值;
(2)试用定义证明:对于任意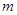 ,
, 在
在 上为单调递增函数;
上为单调递增函数;
(3)若函数 为奇函数,且不等式
为奇函数,且不等式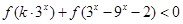 对任意
对任意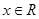 恒成立,求实数
恒成立,求实数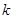 的取值范围。
的取值范围。
(1) m="1"
(2)根据函数单调性,结合定义设出变量,结合作差法得到,变形得到证明。
(3) 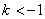
解析试题分析:解:(1)∵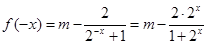 ,且
,且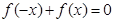
∴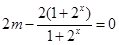 (注:通过
(注:通过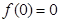 求也同样给分) 3分
求也同样给分) 3分
(2)证明:设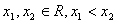 ,则
,则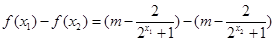
= =
=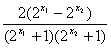
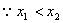 ,
,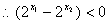
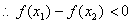 即
即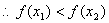 ,所以
,所以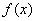 在R上为增函数。 3分
在R上为增函数。 3分
(3)因为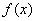 为奇函数且在R上为增函数,
为奇函数且在R上为增函数,
由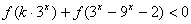 得
得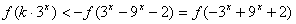
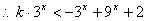 即
即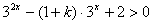 对任意
对任意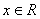 恒成立。
恒成立。
令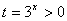 ,问题等价于
,问题等价于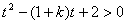 对任意
对任意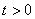 恒成立。
恒成立。
令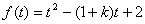 ,其对称轴
,其对称轴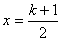 。
。
当 即
即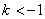 时,
时,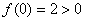 ,符合题意 6分
,符合题意 6分
考点:函数的性质的运用
点评:解决的关键是理解奇函数在x=0处函数值为零,同时能结合函数定义来证明函数单调性,确定结论,属于基础题。

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 为实数,
为实数, ,
, ,求
,求 的单调区间;
的单调区间; ,求
,求
 的最小正周期.
的最小正周期. 时,求函数
时,求函数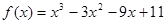
 的递减区间;
的递减区间;
 的不等式
的不等式 ;
; 的图象恒在函数
的图象恒在函数 图象的上方(没有公共点),求
图象的上方(没有公共点),求 的取值范围。
的取值范围。
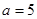 时,求函数
时,求函数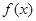 的定义域;
的定义域; 的取值范围。
的取值范围。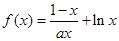
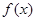 在
在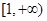 上为增函数,求正实数
上为增函数,求正实数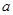 的取值范围;
的取值范围;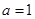 时,求
时,求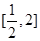 上的最大值和最小值;
上的最大值和最小值;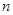 ,都有
,都有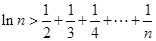 。
。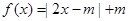 .
. 的解集为
的解集为 ,求实数
,求实数 的值;
的值;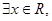 使
使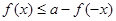 能成立,求实数a的取值范围.
能成立,求实数a的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;
的值; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.