题目内容
已知函数f(x)是R上的偶函数,且满足f(x+1)+f(x)=3,当x∈[0,1]时,f(x)=2-x,则f(-2007.5)的值为
- A.0.5
- B.1.5
- C.-1.5
- D.1
B
分析:先根据题目条件求出函数的周期,然后通过周期性和奇偶性将-2008.5调整到[0,1]内,即可求解.
解答:∵f(x)是定义在R上的偶函数且
f(x+1)+f(x)=3①
∴f(-x+1)+f(-x)=3,
即f(x-1)+f(x)=3②
由①②,得f(x+1)=f(x-1),∴f(x)的周期T=2,
∴f(-2007.5)=f(-2008+0.5)=f(0.5)=2-0.5=1.5.
故选B.
点评:本题是函数性质的综合应用,这一类型的题通常会涉及到周期性、单调性、奇偶性、对称性等.期中周期性的考查通常比较隐蔽,要注意挖掘题中的隐含条件(如f(x+a)=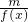 ,f(x+a)=m-f(x)等都能推出函数f(x)的周期T=2a).
,f(x+a)=m-f(x)等都能推出函数f(x)的周期T=2a).
分析:先根据题目条件求出函数的周期,然后通过周期性和奇偶性将-2008.5调整到[0,1]内,即可求解.
解答:∵f(x)是定义在R上的偶函数且
f(x+1)+f(x)=3①
∴f(-x+1)+f(-x)=3,
即f(x-1)+f(x)=3②
由①②,得f(x+1)=f(x-1),∴f(x)的周期T=2,
∴f(-2007.5)=f(-2008+0.5)=f(0.5)=2-0.5=1.5.
故选B.
点评:本题是函数性质的综合应用,这一类型的题通常会涉及到周期性、单调性、奇偶性、对称性等.期中周期性的考查通常比较隐蔽,要注意挖掘题中的隐含条件(如f(x+a)=
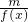 ,f(x+a)=m-f(x)等都能推出函数f(x)的周期T=2a).
,f(x+a)=m-f(x)等都能推出函数f(x)的周期T=2a). 
练习册系列答案
相关题目