Question

（本小题满分12分）已知函数f（x）=(x+3x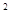+ax+b)e。

(1) 若a = b = 3 ，求f (x) 的单调区间；

(2) 若f (x) 在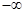（，），（2，）上单调递增，在（，2），（，+）上单调递减，证明：->6。

 

Answer 1

【答案】

解：（1）当a=b= -3时，f（x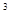）=(x+3x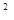-3x-3)e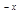，故

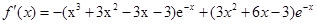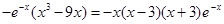=           ……………………………………………………………………………………3分

当x<-3或0<x<3时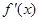，>0;      当-3<x<0或x>3时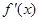，<0,

从而f(x)在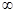（-，-3），（0，3）上单调递增，

在（-3，0），（3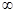，+）上单调递减………………………………………………………. 6分

(2)

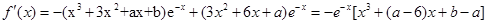
……………………………………………………………………………………...7分

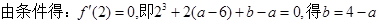…………….……………8分

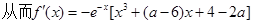
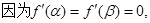
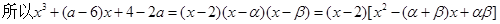
将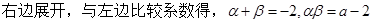……..…..…………….10分

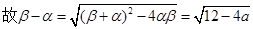………………………………………………..11分

.

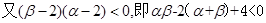由此可得a<-6,于是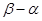>6。…………………………………………………………   12分

 

【解析】略