题目内容
已知曲线C1: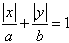 (a>b>0)所围成的封闭图形的面积为
(a>b>0)所围成的封闭图形的面积为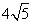 ,曲线C1的内切圆半径为
,曲线C1的内切圆半径为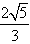 ,记C2为以曲线C1与坐标轴的交点为顶点的椭圆。
,记C2为以曲线C1与坐标轴的交点为顶点的椭圆。
(1)求椭圆C2的标准方程;
(2)设AB是过椭圆C2中心的任意弦,l是线段AB的垂直平分线,M是l上异于椭圆中心的点。
(i)若|MO|=λ|OA|(O为坐标原点),当点A在椭圆C2上运动时,求点M的轨迹方程;
(ii)若M是l与椭圆C2的交点,求△AMB的面积的最小值。
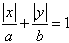 (a>b>0)所围成的封闭图形的面积为
(a>b>0)所围成的封闭图形的面积为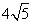 ,曲线C1的内切圆半径为
,曲线C1的内切圆半径为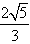 ,记C2为以曲线C1与坐标轴的交点为顶点的椭圆。
,记C2为以曲线C1与坐标轴的交点为顶点的椭圆。(1)求椭圆C2的标准方程;
(2)设AB是过椭圆C2中心的任意弦,l是线段AB的垂直平分线,M是l上异于椭圆中心的点。
(i)若|MO|=λ|OA|(O为坐标原点),当点A在椭圆C2上运动时,求点M的轨迹方程;
(ii)若M是l与椭圆C2的交点,求△AMB的面积的最小值。
解:(1)由题意得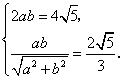
又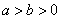
解得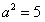 ,
,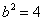
因此所求椭圆的标准方程为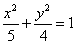 。
。
(2)(i)假设AB所在的直线斜率存在且不为零,设AB所在直线方程为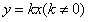 ,
,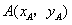
解方程组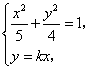 得
得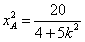 ,
,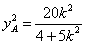
所以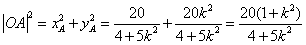
设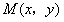 ,由题意知
,由题意知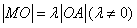 ,
,
所以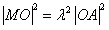 ,
,
即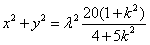 ,
,
因为l是AB的垂直平分线,
所以直线l的方程为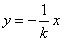 ,
,
即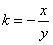 ,
,
因此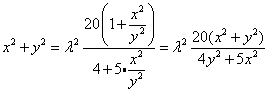 ,
,
又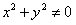 ,
,
所以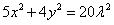 ,
,
故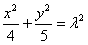
又当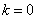 或不存在时,上式仍然成立
或不存在时,上式仍然成立
综上所述,M的轨迹方程为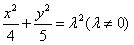 。
。
(2)当k存在且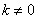 时,由(i)得
时,由(i)得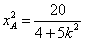 ,
,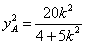 ,
,
由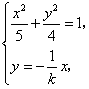 解得
解得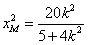 ,
,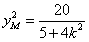 ,
,
所以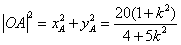 ,
,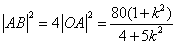 ,
,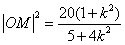
由于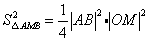
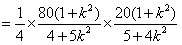
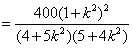
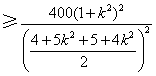
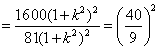 ,
,
当且仅当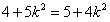 时等号成立,即
时等号成立,即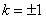 时等号成立,
时等号成立,
此时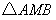 面积的最小值是
面积的最小值是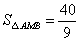
当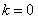 ,
,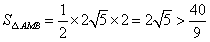
当k不存在时,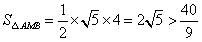
综上所述,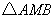 的面积的最小值为
的面积的最小值为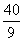 。
。
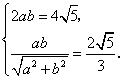
又
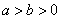
解得
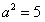 ,
,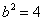
因此所求椭圆的标准方程为
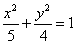 。
。(2)(i)假设AB所在的直线斜率存在且不为零,设AB所在直线方程为
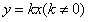 ,
,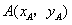
解方程组
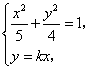 得
得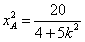 ,
,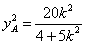
所以
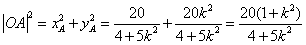
设
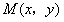 ,由题意知
,由题意知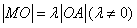 ,
,所以
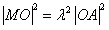 ,
,即
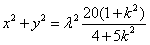 ,
,因为l是AB的垂直平分线,
所以直线l的方程为
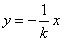 ,
,即
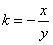 ,
,因此
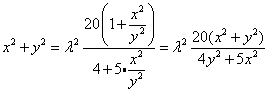 ,
,又
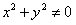 ,
,所以
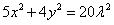 ,
,故
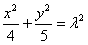
又当
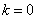 或不存在时,上式仍然成立
或不存在时,上式仍然成立综上所述,M的轨迹方程为
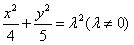 。
。(2)当k存在且
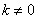 时,由(i)得
时,由(i)得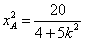 ,
,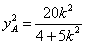 ,
,由
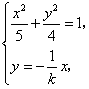 解得
解得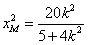 ,
,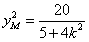 ,
,所以
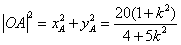 ,
,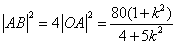 ,
,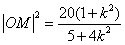
由于
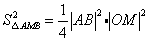
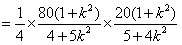
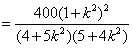
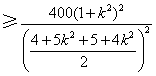
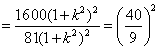 ,
,当且仅当
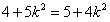 时等号成立,即
时等号成立,即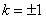 时等号成立,
时等号成立,此时
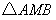 面积的最小值是
面积的最小值是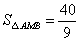
当
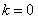 ,
,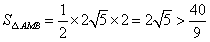
当k不存在时,
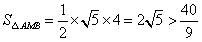
综上所述,
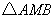 的面积的最小值为
的面积的最小值为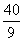 。
。
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目