题目内容
如图,已知点P是边长为1的正方形ABCD所在平面外一点,且PA⊥平面ABCD,点E为PD中点.(1)求证:PB∥平面EAC;
(2)求异面直线PB与AC所成的角的取值范围.

【答案】分析:(1)连结BD交AC于O点,连结EO,根据OE是三角形PBD的中位线可得EO∥PB,再利用直线和平面平行的判定定理证得 PB∥平面ACE.
(2)设PA=x,求得PB=PD=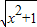 ,AE=
,AE= ,OE=
,OE=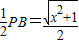 ,可得△AEO为等腰三角形,且∠EAO=∠EOA.由此可得∠EOA即为异面直线PB与AC所成的角.取OA的中点M,在Rt△EMO中,求得cos∠EOA=
,可得△AEO为等腰三角形,且∠EAO=∠EOA.由此可得∠EOA即为异面直线PB与AC所成的角.取OA的中点M,在Rt△EMO中,求得cos∠EOA=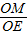 的范围,可得直线PB与AC所成的角的取值范围.
的范围,可得直线PB与AC所成的角的取值范围.
解答: (1)证明:连结BD交AC于O点,连结EO,
(1)证明:连结BD交AC于O点,连结EO,
因为点E为PD中点,点O为BD中点,故OE是三角形PBD的中位线.
所以EO∥PB,又PB不在平面ACE上,
EO在平面ACE内,所以PB∥平面ACE. …(6分)
(2)解:设PA=x,则PB=PD=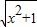 ,
,
在Rt△PAD中,AE是其中线,AE=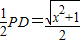 ,
,
在△PBD中,OE是其中位线,OE=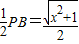 ,
,
所以△AEO为等腰三角形,且∠EAO=∠EOA.…(8分)
∵EO∥PB,则∠EOA即为异面直线PB与AC所成的角.…(10分)
取OA的中点M,则EM⊥AO,在Rt△EMO中,
cos∠EOA=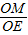 =
= =
=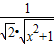 ,(x>0).
,(x>0).
∵x2+1>1,∴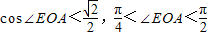 ,
,
所以异面直线PB与AC所成的角的取值范围是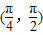 .…(12分)
.…(12分)
点评:本题主要考查直线和平面平行的判定定理的应用,异面直线所成的角的定义和求法,属于中档题.
(2)设PA=x,求得PB=PD=
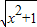 ,AE=
,AE= ,OE=
,OE=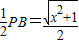 ,可得△AEO为等腰三角形,且∠EAO=∠EOA.由此可得∠EOA即为异面直线PB与AC所成的角.取OA的中点M,在Rt△EMO中,求得cos∠EOA=
,可得△AEO为等腰三角形,且∠EAO=∠EOA.由此可得∠EOA即为异面直线PB与AC所成的角.取OA的中点M,在Rt△EMO中,求得cos∠EOA=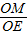 的范围,可得直线PB与AC所成的角的取值范围.
的范围,可得直线PB与AC所成的角的取值范围.解答:
 (1)证明:连结BD交AC于O点,连结EO,
(1)证明:连结BD交AC于O点,连结EO,因为点E为PD中点,点O为BD中点,故OE是三角形PBD的中位线.
所以EO∥PB,又PB不在平面ACE上,
EO在平面ACE内,所以PB∥平面ACE. …(6分)
(2)解:设PA=x,则PB=PD=
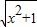 ,
,在Rt△PAD中,AE是其中线,AE=
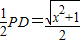 ,
,在△PBD中,OE是其中位线,OE=
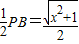 ,
,所以△AEO为等腰三角形,且∠EAO=∠EOA.…(8分)
∵EO∥PB,则∠EOA即为异面直线PB与AC所成的角.…(10分)
取OA的中点M,则EM⊥AO,在Rt△EMO中,
cos∠EOA=
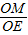 =
= =
=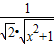 ,(x>0).
,(x>0).∵x2+1>1,∴
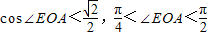 ,
,所以异面直线PB与AC所成的角的取值范围是
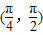 .…(12分)
.…(12分)点评:本题主要考查直线和平面平行的判定定理的应用,异面直线所成的角的定义和求法,属于中档题.

练习册系列答案
相关题目
 某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2.
某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2. 如图,已知点P是边长为1的正方形ABCD所在平面外一点,且PA⊥平面ABCD,点E为PD中点.
如图,已知点P是边长为1的正方形ABCD所在平面外一点,且PA⊥平面ABCD,点E为PD中点.
