题目内容
在O为坐标原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知 且点B的纵坐标大于零.
且点B的纵坐标大于零.(1)求圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
(2)设直线l平行于直线AB且过点(0,a),问是否存在实数a,使得椭圆
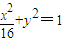 上有两个不同的点关于直线l对称,若不存在,请说明理由;若存在,请求出实数a的取值范围.
上有两个不同的点关于直线l对称,若不存在,请说明理由;若存在,请求出实数a的取值范围.
【答案】分析:(1)先利用条件求点B的坐标以及直线OB的方程,再利用关于直线对称的圆的方程的求法即可求出圆x2-6x+y2+2y=0关于直线OB对称的圆的方程;
(2)先求出直线l的方程以及关于直线l对称的两点的坐标和直线l的方程之间的关系,再利用判别式的范围来求实数a的取值范围.
解答:解:(1)设点B为(x,y),因为点A(4,-3)为△OAB的直角顶点和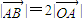 .
.
所以OA⊥AB且|OB|=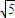 |OA|⇒
|OA|⇒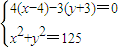 ⇒
⇒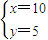 (因点B的纵坐标大于零另一组舍去)
(因点B的纵坐标大于零另一组舍去)
所以直线OB的方程为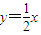 .
.
又圆x2-6x+y2+2y=0⇒(x-3)2+(y+1)2=10.
圆心(3,-1)关于直线OB的对称点为(1,3).
所以圆x2-6x+y2+2y=0关于直线OB对称的圆的方程为(x-1)2+(y-3)2=10.
(2)因为kAB= ,所以直线l的方程为y=
,所以直线l的方程为y= x+a.
x+a.
则椭圆 上关于直线l对称的两个不同的点M(m,n),N(b,c)在直线y=-
上关于直线l对称的两个不同的点M(m,n),N(b,c)在直线y=- x+d上,
x+d上,
由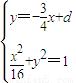 ⇒
⇒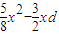 +d2-1=0.△=
+d2-1=0.△=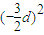 -4×
-4×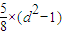 >0⇒d2<10①.
>0⇒d2<10①.
且m+b=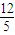 d,所以c+n=-
d,所以c+n=- (m+b)+2d=
(m+b)+2d=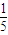 d,
d,
所以M,N的中点为(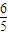 d,
d,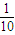 d)在y=
d)在y= x+a上.
x+a上.
解得d=- a代入①⇒
a代入①⇒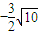 <a<
<a<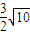 .
.
故存在满足题意的实数a,其取值范围为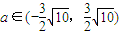 .
.
点评:在圆锥曲线的综合大题中,主要考查解析几何的有关知识,以及分析问题与解决问题的能力.值得引起重视的一个现象是,经常出现一条或几条直线与两种圆锥曲线(包括圆)的位置关系问题,同时要注意其与平面几何、平面向量以及导数的知识的综合命题.
(2)先求出直线l的方程以及关于直线l对称的两点的坐标和直线l的方程之间的关系,再利用判别式的范围来求实数a的取值范围.
解答:解:(1)设点B为(x,y),因为点A(4,-3)为△OAB的直角顶点和
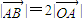 .
.所以OA⊥AB且|OB|=
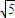 |OA|⇒
|OA|⇒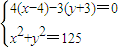 ⇒
⇒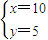 (因点B的纵坐标大于零另一组舍去)
(因点B的纵坐标大于零另一组舍去)所以直线OB的方程为
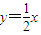 .
.又圆x2-6x+y2+2y=0⇒(x-3)2+(y+1)2=10.
圆心(3,-1)关于直线OB的对称点为(1,3).
所以圆x2-6x+y2+2y=0关于直线OB对称的圆的方程为(x-1)2+(y-3)2=10.
(2)因为kAB=
 ,所以直线l的方程为y=
,所以直线l的方程为y= x+a.
x+a.则椭圆
 上关于直线l对称的两个不同的点M(m,n),N(b,c)在直线y=-
上关于直线l对称的两个不同的点M(m,n),N(b,c)在直线y=- x+d上,
x+d上,由
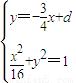 ⇒
⇒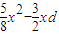 +d2-1=0.△=
+d2-1=0.△=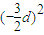 -4×
-4×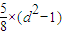 >0⇒d2<10①.
>0⇒d2<10①.且m+b=
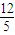 d,所以c+n=-
d,所以c+n=- (m+b)+2d=
(m+b)+2d=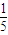 d,
d,所以M,N的中点为(
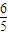 d,
d,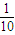 d)在y=
d)在y= x+a上.
x+a上.解得d=-
 a代入①⇒
a代入①⇒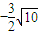 <a<
<a<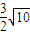 .
.故存在满足题意的实数a,其取值范围为
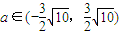 .
.点评:在圆锥曲线的综合大题中,主要考查解析几何的有关知识,以及分析问题与解决问题的能力.值得引起重视的一个现象是,经常出现一条或几条直线与两种圆锥曲线(包括圆)的位置关系问题,同时要注意其与平面几何、平面向量以及导数的知识的综合命题.

练习册系列答案
相关题目
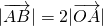 且点B的纵坐标大于零.
且点B的纵坐标大于零.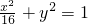 上有两个不同的点关于直线l对称,若不存在,请说明理由;若存在,请求出实数a的取值范围.
上有两个不同的点关于直线l对称,若不存在,请说明理由;若存在,请求出实数a的取值范围.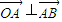 ,点A(4,-3),B点在第一象限且到x轴的距离为5.
,点A(4,-3),B点在第一象限且到x轴的距离为5.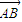 的坐标及OB所在的直线方程;
的坐标及OB所在的直线方程;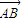 为方向向量且过(0,a)点,问是否存在实数a,使得椭圆
为方向向量且过(0,a)点,问是否存在实数a,使得椭圆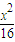 +y2=1上有两个不同的点关于直线l对称.若不存在,请说明理由; 存在请求出实数a的取值范围.
+y2=1上有两个不同的点关于直线l对称.若不存在,请说明理由; 存在请求出实数a的取值范围.