题目内容
在以O为坐标原点的直角坐标系中,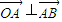 ,点A(4,-3),B点在第一象限且到x轴的距离为5.
,点A(4,-3),B点在第一象限且到x轴的距离为5.(1) 求向量
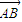 的坐标及OB所在的直线方程;
的坐标及OB所在的直线方程;(2) 求圆(x-3)2+(y+1)2=10关于直线OB对称的圆的方程;
(3) 设直线l
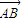 为方向向量且过(0,a)点,问是否存在实数a,使得椭圆
为方向向量且过(0,a)点,问是否存在实数a,使得椭圆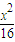 +y2=1上有两个不同的点关于直线l对称.若不存在,请说明理由; 存在请求出实数a的取值范围.
+y2=1上有两个不同的点关于直线l对称.若不存在,请说明理由; 存在请求出实数a的取值范围.
【答案】分析:(1)设B(x,5),则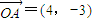 ,
, ,由
,由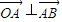 ,可得4(x-4)-24=0,x=10,由此能够求出向量
,可得4(x-4)-24=0,x=10,由此能够求出向量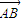 的坐标及OB所在的直线方程.
的坐标及OB所在的直线方程.
(2)设圆心关于直线OB的对称点坐标为(x1,y1),由(x-3)2+(y+1)2=10,可知圆心为(3,-1),半径为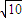 .由方程
.由方程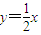 知
知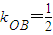 ,由此能够推导出所求圆的方程.
,由此能够推导出所求圆的方程.
(3)假设椭圆上存在两点P(x1,y1),Q(x2,y2)关于直线l对称,设其中点坐标为M(x,y)由已知直线l的方程为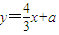 ,可设直线AB的方程为
,可设直线AB的方程为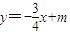 ,将其与已知椭圆方程联立得5x2-12mx+8m2-8=0.再由韦达定理进行求解.
,将其与已知椭圆方程联立得5x2-12mx+8m2-8=0.再由韦达定理进行求解.
解答:解:(1)设B(x,5),
则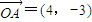 ,
,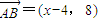 ,
,
由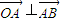 ,可得
,可得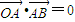 ,
,
∴4(x-4)-24=0,x=10,
∴B(10,5),∴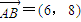 ,
,
OB所在的直线方程是: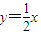 (5分)
(5分)
(2)设圆心关于直线OB的对称点坐标为(x1,y1),
由(x-3)2+(y+1)2=10,
可知圆心为(3,-1),半径为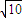 .
.
由方程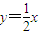 知
知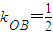 ,
,
∴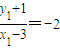 ,又点
,又点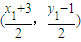 在
在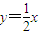 上
上
∴得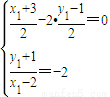 ,∴
,∴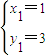 ,
,
故所求圆的方程为(x-1)2+(y-3)2=10.(10分)
(3)假设椭圆上存在两点P(x1,y1),Q(x2,y2)关于直线l对称,
设其中点坐标为M(x,y),
由已知直线l的方程为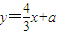 ,
,
可设直线AB的方程为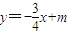
将其与已知椭圆方程联立,
得5x2-12mx+8m2-8=0.
由韦达定理知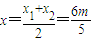 ,
,
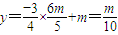 .(12分)
.(12分)
中点M(x,y)在圆的内部可知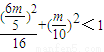 ,
,
解得m2<10.
又M(x,y)在直线l上,
故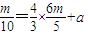 ,
,
解得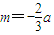 代入m2<10
代入m2<10
解得 ,
,
即存在满足题意的实数a,
其取值范围为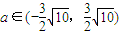 .(16分)
.(16分)
点评:本题考查圆的性质和应用,解题时要认真审题,仔细解答,注意合理地选取用公式.
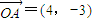 ,
, ,由
,由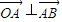 ,可得4(x-4)-24=0,x=10,由此能够求出向量
,可得4(x-4)-24=0,x=10,由此能够求出向量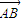 的坐标及OB所在的直线方程.
的坐标及OB所在的直线方程.(2)设圆心关于直线OB的对称点坐标为(x1,y1),由(x-3)2+(y+1)2=10,可知圆心为(3,-1),半径为
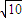 .由方程
.由方程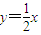 知
知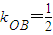 ,由此能够推导出所求圆的方程.
,由此能够推导出所求圆的方程.(3)假设椭圆上存在两点P(x1,y1),Q(x2,y2)关于直线l对称,设其中点坐标为M(x,y)由已知直线l的方程为
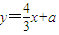 ,可设直线AB的方程为
,可设直线AB的方程为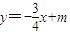 ,将其与已知椭圆方程联立得5x2-12mx+8m2-8=0.再由韦达定理进行求解.
,将其与已知椭圆方程联立得5x2-12mx+8m2-8=0.再由韦达定理进行求解.解答:解:(1)设B(x,5),
则
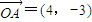 ,
,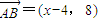 ,
,由
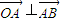 ,可得
,可得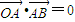 ,
,∴4(x-4)-24=0,x=10,
∴B(10,5),∴
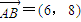 ,
,OB所在的直线方程是:
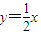 (5分)
(5分)(2)设圆心关于直线OB的对称点坐标为(x1,y1),
由(x-3)2+(y+1)2=10,
可知圆心为(3,-1),半径为
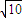 .
.由方程
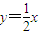 知
知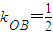 ,
,∴
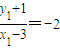 ,又点
,又点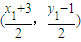 在
在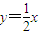 上
上∴得
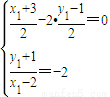 ,∴
,∴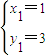 ,
,故所求圆的方程为(x-1)2+(y-3)2=10.(10分)
(3)假设椭圆上存在两点P(x1,y1),Q(x2,y2)关于直线l对称,
设其中点坐标为M(x,y),
由已知直线l的方程为
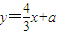 ,
,可设直线AB的方程为
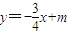
将其与已知椭圆方程联立,
得5x2-12mx+8m2-8=0.
由韦达定理知
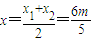 ,
,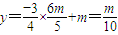 .(12分)
.(12分)中点M(x,y)在圆的内部可知
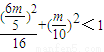 ,
,解得m2<10.
又M(x,y)在直线l上,
故
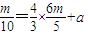 ,
,解得
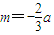 代入m2<10
代入m2<10解得
 ,
,即存在满足题意的实数a,
其取值范围为
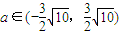 .(16分)
.(16分)点评:本题考查圆的性质和应用,解题时要认真审题,仔细解答,注意合理地选取用公式.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
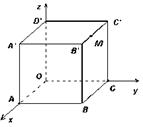
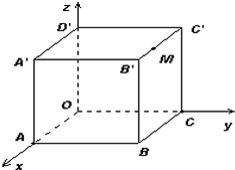 11、如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
11、如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
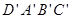 ,点M在
,点M在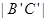 上,且
上,且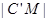
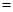 2
2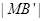 ,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 .
,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 .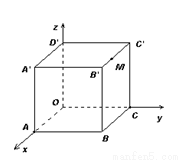
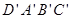 ,点M在
,点M在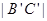 上,且
上,且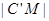
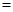 2
2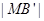 ,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
.
,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为
.
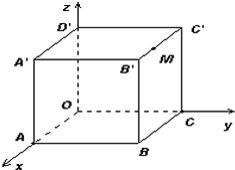 如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.
如图,棱长为3a正方体OABC-D'A'B'C',点M在|B'C'|上,且|C'M|=2|MB'|,以O为坐标原点,建立如图空间直有坐标系,则点M的坐标为 ________.