题目内容
参数方程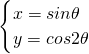 (θ为参数)所表示的曲线的普通方程为________.
(θ为参数)所表示的曲线的普通方程为________.
y=1-2x2(-1≤x≤1)
分析:由条件并利用 cos2θ=1-2sin2θ,可得 y=1-2x2,-1≤x≤1.
解答:因为cos2θ=1-2sin2θ,∴y=1-2x2,-1≤x≤1,
故答案为:y=1-2x2,(-1≤x≤1).
点评:本题考查二倍角的余弦公式,把参数方程化为普通方程的方法,利用cos2θ=1-2sin2θ,是解题的关键.
分析:由条件并利用 cos2θ=1-2sin2θ,可得 y=1-2x2,-1≤x≤1.
解答:因为cos2θ=1-2sin2θ,∴y=1-2x2,-1≤x≤1,
故答案为:y=1-2x2,(-1≤x≤1).
点评:本题考查二倍角的余弦公式,把参数方程化为普通方程的方法,利用cos2θ=1-2sin2θ,是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 (
( (t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是( )
(t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是( )



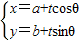 (t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是( )
(t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是( )
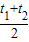


 .
. (α为参数),点Q极坐标为
(α为参数),点Q极坐标为 .
. .
. (α为参数),点Q极坐标为
(α为参数),点Q极坐标为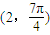 .
.