题目内容
(1)选修4-2:矩阵与变换设矩阵
 .
.(I)若a=2,b=3,求矩阵M的逆矩阵M-1;
(II)若曲线C:x2+4xy+2y2=1在矩阵M的作用下变换成曲线C':x2-2y2=1,求a+b的值.
(2)选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合.圆C的参数方程为
 (α为参数),点Q极坐标为
(α为参数),点Q极坐标为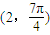 .
.(Ⅰ)化圆C的参数方程为极坐标方程;
(Ⅱ)若点P是圆C上的任意一点,求P、Q两点距离的最小值.
(3)选修4-5:不等式选讲
设函数f(x)=|x+1|+|x-2|.
(Ⅰ)求y=f(x)的最小值;
(Ⅱ)若关于x的不等式f(x)≥4的解集为A,求集合A.
【答案】分析:(1)(I)设矩阵M的逆矩阵 ,则
,则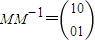 ,建立方程组,即可求得所求的逆矩阵;
,建立方程组,即可求得所求的逆矩阵;
(II)设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P'(x',y'),可得 ,利用点P'(x',y')在曲线C'上,可得曲线C的方程,根据已知曲线C的方程,比较系数可得结论;
,利用点P'(x',y')在曲线C'上,可得曲线C的方程,根据已知曲线C的方程,比较系数可得结论;
(2)(I)先求圆C的普通方程,展开,再化为极坐标方程;
(II)点Q的直角坐标为(2,-2),且点Q在圆C内,求出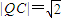 ,可得P,Q两点距离的最小值;
,可得P,Q两点距离的最小值;
(3)(I)利用绝对值的运用,写出分段函数,从而可求y=f(x)的最小值;
(II)利用分段函数,根据f(x)≥4,列出不等式,即可求得不等式f(x)≥4的解集.
解答:(1)(本小题满分7分)选修4-2:矩阵与变换
解:(I)设矩阵M的逆矩阵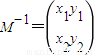 ,则
,则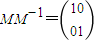 .又
.又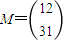 ,
,
所以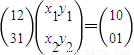 ,所以x1+2x2=1,3x1+x2=0,y1+2y2=0,3y1+y2=1,
,所以x1+2x2=1,3x1+x2=0,y1+2y2=0,3y1+y2=1,
即 ,
,
故所求的逆矩阵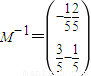 .…(4分)
.…(4分)
(II)设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P'(x',y'),则
 ,即
,即 ,…(5分)
,…(5分)
又点P'(x',y')在曲线C'上,所以x'2-2y'2=1,则(x+ay)2-2(bx+y)2=1,
即(1-2b2)x2+(2a-4b)xy+(a2-2)y2=1为曲线C的方程,
又已知曲线C的方程为x2+4xy+2y2=1,
比较系数可得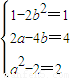 ,解得b=0,a=2,∴a+b=2.…(7分)
,解得b=0,a=2,∴a+b=2.…(7分)
(2)(本小题满分7分)选修4-4:坐标系与参数方程
解:(I)圆C普通方程为(x-1)2+(y+1)2=4,
展开得x2+y2-2x+2y-2=0,…(2分)
化为极坐标方程为ρ2-2ρcosθ+2ρsinθ-2=0. …(4分)
(II)点Q的直角坐标为(2,-2),且点Q在圆C内,
因为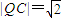 ,所以P,Q两点距离的最小值为
,所以P,Q两点距离的最小值为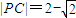 . …(7分)
. …(7分)
(3)(本小题满分7分)选修4-5:不等式选讲
解:(I)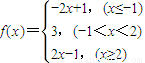 所以y=f(x)的最小值为3.…(4分)
所以y=f(x)的最小值为3.…(4分)
(II) 由(I)可知,当x≤-1时,f(x)≥4,即-2x+1≥4,此时 ;
;
当x≥2时,f(x)≥4,即2x-1≥4,此时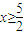 .
.
因此不等式f(x)≥4的解集为A为{|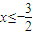 或
或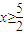 }. …(7分)
}. …(7分)
点评:本题考查选修知识,考查矩阵与变换,考查坐标系与参数方程,考查不等式选讲,综合性强.
 ,则
,则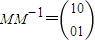 ,建立方程组,即可求得所求的逆矩阵;
,建立方程组,即可求得所求的逆矩阵;(II)设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P'(x',y'),可得
 ,利用点P'(x',y')在曲线C'上,可得曲线C的方程,根据已知曲线C的方程,比较系数可得结论;
,利用点P'(x',y')在曲线C'上,可得曲线C的方程,根据已知曲线C的方程,比较系数可得结论;(2)(I)先求圆C的普通方程,展开,再化为极坐标方程;
(II)点Q的直角坐标为(2,-2),且点Q在圆C内,求出
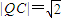 ,可得P,Q两点距离的最小值;
,可得P,Q两点距离的最小值;(3)(I)利用绝对值的运用,写出分段函数,从而可求y=f(x)的最小值;
(II)利用分段函数,根据f(x)≥4,列出不等式,即可求得不等式f(x)≥4的解集.
解答:(1)(本小题满分7分)选修4-2:矩阵与变换
解:(I)设矩阵M的逆矩阵
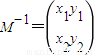 ,则
,则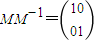 .又
.又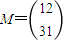 ,
,所以
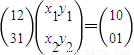 ,所以x1+2x2=1,3x1+x2=0,y1+2y2=0,3y1+y2=1,
,所以x1+2x2=1,3x1+x2=0,y1+2y2=0,3y1+y2=1,即
 ,
,故所求的逆矩阵
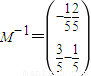 .…(4分)
.…(4分)(II)设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P'(x',y'),则

 ,即
,即 ,…(5分)
,…(5分)又点P'(x',y')在曲线C'上,所以x'2-2y'2=1,则(x+ay)2-2(bx+y)2=1,
即(1-2b2)x2+(2a-4b)xy+(a2-2)y2=1为曲线C的方程,
又已知曲线C的方程为x2+4xy+2y2=1,
比较系数可得
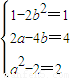 ,解得b=0,a=2,∴a+b=2.…(7分)
,解得b=0,a=2,∴a+b=2.…(7分)(2)(本小题满分7分)选修4-4:坐标系与参数方程
解:(I)圆C普通方程为(x-1)2+(y+1)2=4,
展开得x2+y2-2x+2y-2=0,…(2分)
化为极坐标方程为ρ2-2ρcosθ+2ρsinθ-2=0. …(4分)
(II)点Q的直角坐标为(2,-2),且点Q在圆C内,
因为
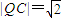 ,所以P,Q两点距离的最小值为
,所以P,Q两点距离的最小值为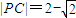 . …(7分)
. …(7分)(3)(本小题满分7分)选修4-5:不等式选讲
解:(I)
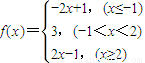 所以y=f(x)的最小值为3.…(4分)
所以y=f(x)的最小值为3.…(4分)(II) 由(I)可知,当x≤-1时,f(x)≥4,即-2x+1≥4,此时
 ;
;当x≥2时,f(x)≥4,即2x-1≥4,此时
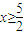 .
.因此不等式f(x)≥4的解集为A为{|
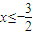 或
或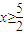 }. …(7分)
}. …(7分)点评:本题考查选修知识,考查矩阵与变换,考查坐标系与参数方程,考查不等式选讲,综合性强.

练习册系列答案
相关题目
 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA, ,PD=1,BD=8,求线段BC的长.
,PD=1,BD=8,求线段BC的长. ,矩阵阵
,矩阵阵 ,
, ,求在矩阵
,求在矩阵 作用下变换所得到的图形的面积.
作用下变换所得到的图形的面积. (
( 为参数,
为参数, 为常数且
为常数且 )被以原点为极点,
)被以原点为极点, 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长. ,求证:
,求证: .
.