题目内容
已知集合A={x||x|≤2,x∈R},B={x| ≤2,x∈Z},则A∩B=
≤2,x∈Z},则A∩B=
A.(0,2) B.[0,2] C.{0,2} D.{0,1,2}
【答案】
D
【解析】
试题分析:解:由集合A中的不等式|x|≤2,解得:-2≤x≤2,所以集合A=[-2,2],由集合B中的不等式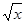 ≤2,解得:0≤x≤4,又x∈Z,所以集合B={0,1,2,3,4},则A∩B={0,1,2}.故选D
≤2,解得:0≤x≤4,又x∈Z,所以集合B={0,1,2,3,4},则A∩B={0,1,2}.故选D
考点:交集
点评:解得本题的关键是确定出两集合,方法是求出两集合中其他不等式的解集.学生容易出错的地方是忽略负数没有平方根这个条件,没有找全集合B中的元素

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目