题目内容
(2009•台州二模)下图是几何体ABC-A1B1C1的三视图和直观图.M是CC1上的动点,N,E分别是AM,A1B1的中点.
(1)求证:NE∥平面BB1C1C;
(2)当M在CC1的什么位置时,B1M与平面AA1C1C所成的角是30°.

(1)求证:NE∥平面BB1C1C;
(2)当M在CC1的什么位置时,B1M与平面AA1C1C所成的角是30°.

分析:(1)利用三角形中位线的性质,可得线线平行,从而可得线面平行;
(2)过B1作B1F⊥A1C1,连接FM,可得∠B1MF为B1M与平面AA1C1C所成的角,求出B1M的长,即可得到结论.
(2)过B1作B1F⊥A1C1,连接FM,可得∠B1MF为B1M与平面AA1C1C所成的角,求出B1M的长,即可得到结论.
解答: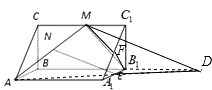 (1)证明:连接AE并延长交BB1于点D,连接DM,则NE为三角形ADM的中位线
(1)证明:连接AE并延长交BB1于点D,连接DM,则NE为三角形ADM的中位线
∴NE∥DM
∵NE?平面BB1C1C,DM?平面BB1C1C
∴NE∥平面BB1C1C;
(2)解:过B1作B1F⊥A1C1,连接FM,则
∵AA1⊥平面A1B1C1,B1F?平面A1B1C1,
∴AA1⊥B1F
∵A1C1∩AA1=A1,∴B1F⊥平面AA1C1C
∴∠B1MF为B1M与平面AA1C1C所成的角,即∠B1MF=30°
∵A1B1=B1C1=2,A1B1⊥B1C1,∴B1F=
∴B1M=2
∴C1M=2
∵CC1=4,
∴M是CC1的中点时,B1M与平面AA1C1C所成的角是30°.
 (1)证明:连接AE并延长交BB1于点D,连接DM,则NE为三角形ADM的中位线
(1)证明:连接AE并延长交BB1于点D,连接DM,则NE为三角形ADM的中位线∴NE∥DM
∵NE?平面BB1C1C,DM?平面BB1C1C
∴NE∥平面BB1C1C;
(2)解:过B1作B1F⊥A1C1,连接FM,则
∵AA1⊥平面A1B1C1,B1F?平面A1B1C1,
∴AA1⊥B1F
∵A1C1∩AA1=A1,∴B1F⊥平面AA1C1C
∴∠B1MF为B1M与平面AA1C1C所成的角,即∠B1MF=30°
∵A1B1=B1C1=2,A1B1⊥B1C1,∴B1F=
| 2 |
∴B1M=2
| 2 |
∴C1M=2
∵CC1=4,
∴M是CC1的中点时,B1M与平面AA1C1C所成的角是30°.
点评:本题考查线面平行,考查线面角,考查学生的计算能力,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目